HOW TO FIND LENGTH OF SIDES OF A KITE

Definition of kite :

A kite is a quadrilateral which has two pairs of adjacent sides equal in length.

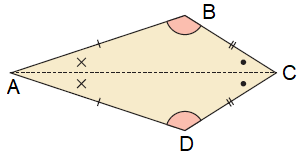
In the kite given above,

AB = AC and BC = DC

Find the values of the variables. Then find the lengths of the sides.

Problem 1 :

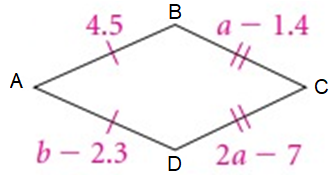
Solution :

AB = 4.5, AD = b - 2.3

AB = AD

4.5 = b – 2.3

Add 2.3 to both sides.

4.5 + 2.3 = b – 2.3 + 2.3

6.8 = b

b = 6.8

BC = DC

a – 1.4 = 2a – 7

Comparing like terms.

a – 2a = -7 + 1.4

-a = -5.6

a = 5.6

BC = a - 1.4

Applying the value of a, we get

BC = 5.6 - 1.4

BC = 4.2

So, the lengths of the sides are

AB = 4.5, AD = 4.5, BC = 4.2 and DC = 4.2

Problem 2 :

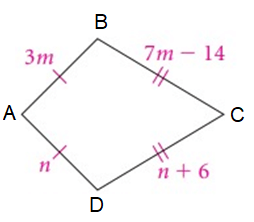
Solution :

By observing the figure,

3m = n

3m - n = 0 ----(1)

7m - 14 = n + 6

7m - n = 6 + 14

7m - n = 20 -----(2)

(1) - (2)

3m - n - (7m - n) = 0 - 20

3m - n - 7m + n = -20

-4m = -20

m = 5

By applying the value of m in (1), we get

3(15) = n

n = 45

AB = 3m ==> 3(5) ==> 15

AB and AD is 15.

DC = n + 6

DC = 45 + 6 ==> 51

BC and DC are 51.

Problem 3 :

Determine the value of x for which EFGH is a kite.

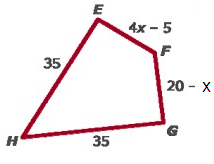
Solution :

EF = FG

4x – 5 = 20 – x

Comparing like terms.

4x + x = 20 + 5

5x = 25

Divide both sides by 5.

5x/5 = 25/5

x = 5

So, the value of x is 5.

Problem 4 :

Find the value of x in the following kite.

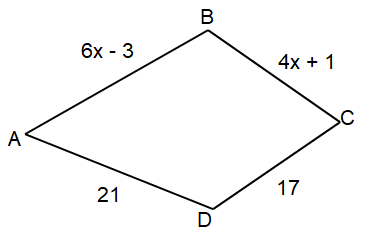
Solution :

Since it kite,

AB = AD and BC = DC

6x - 3 = 21

6x = 21 + 3

6x = 24

x = 24/6

x = 4