HOW TO FIND INTERVALS OF CONTINUITY ON A GRAPH

To find intervals of continuity from a graph, we should have clear understanding about

What is continuity ?
How to find continuity of the function from graph ?

What is continuity ?

In mathematics, a continuous function has much the same meaning. The graph of a continuous function does not have interrupting breaks, such as holes, gaps, or jumps. Thus, the graph of a continuous function can be drawn without lifting a pencil off the paper.

The three graphs that cannot be drawn without lifting a pencil from the paper. In each case, there appears to be an interruption of the graph of at f x = a.

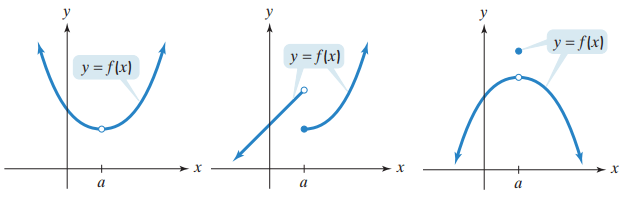
Limit is not defined:

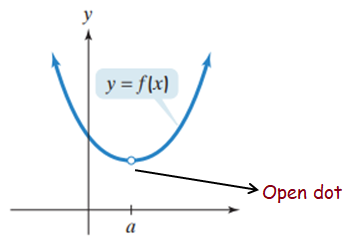
The interruption occurs because the open dot indicates there is no point on the graph corresponding to this, shows that is not defined.

Limit does not exist :

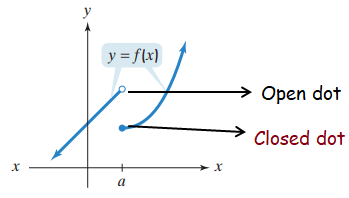
The closed blue dot, it shows that is defined. However, there is a jump at as x approaches from the left, the values of f(x) get closer to the point shown by the open dot.

By contrast, as x approaches from the right, the values of f(x) get closer to the point shown by the closed dot.

There is no single limit as x approaches. The jump in the graph reflects the fact that does not exist

Limits is not equal :

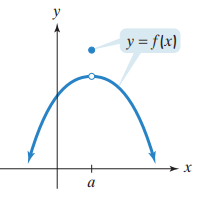
The closed blue dot at shows that is defined. Furthermore, as x approaches from the left or from the right, the values of f(x) get closer to the of the point shown by the open dot.

Thus, exists. However, there is still an interruption at a. Do you see why? The limit as x approaches is the open dot. By contrast, the value of the function at x = a is the closed dot. The interruption in the graph reflects the fact that and are not equal.

We now provide a precise definition of what it means for a function to be continuous at a number.

Conditions :

A function is continuous at when three conditions are satisfied.

1. f is defined at that is, is in the domain of so that is a real number.

2. lim_x-->a f(x) exists.

3. lim _{x--> a} f(x) = f(a)

Find the intervals on which each function is continuous.

Problem 1 :

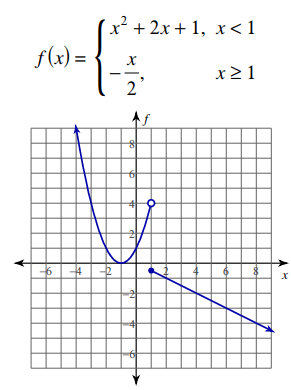
Solution :

From -∞ to 1, the graph doesn't have any break.
From 1 to ∞, the graph doesn't have any break.

Type of discontinuity :

At x = 1, there is a jump discontinuity.

So, the given function is continuous in the interval

(-∞, 1) U [1, ∞)

Problem 2 :

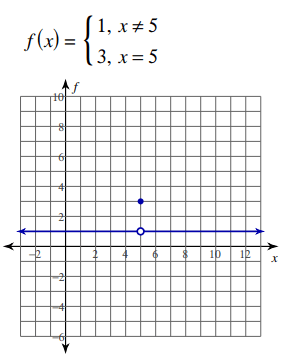
Solution :

From -∞ to 5, the graph doesn't have any break.
From 5 to ∞, the graph doesn't have any break.

Limit is not equal :

At x = 5, the limits is not equal

So, the given function is continuous in the interval

(-∞, 5) U (5, ∞)

Problem 3 :

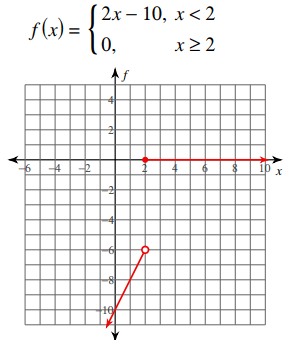
Solution :

From -∞ to 2, the graph doesn't have any break.
From 2 to ∞, the graph doesn't have any break.

Type of discontinuity :

We have jump discontinuity at x = 2.

So, the given function is continuous in the interval

(-∞, 2) U (2, ∞)

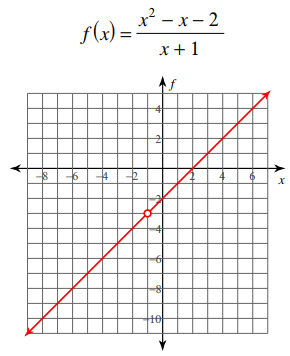
Solution :

From -∞ to -1, the graph doesn't have any break.
From 1 to ∞, the graph doesn't have any break.

Type of discontinuity :

There is a hole at x = -1

So, the given function is continuous in the interval

(-∞, -1) U (-1, ∞)

HOW TO FIND INTERVALS OF CONTINUITY ON A GRAPH

Limit is not defined:

Limit does not exist :

Limits is not equal :

Conditions :

Recent Articles

Finding Range of Values Inequality Problems

Solving Two Step Inequality Word Problems

Exponential Function Context and Data Modeling