HOW TO FIND FOG AND GOF FROM THE GIVEN RELATIONS F AND G

Problem 1 :

Let f = {(3, 1), (9, 3), (12, 4)} and g = {(1, 3) (3, 3) (4, 9) (5, 9)}

Show that gof and fog are defined. Also find fog and gof.

Solution :

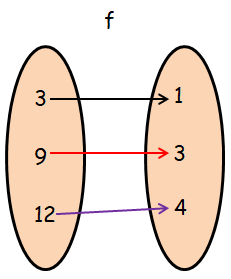
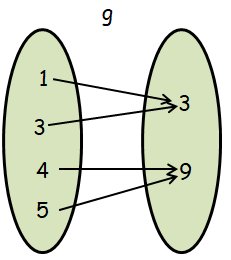
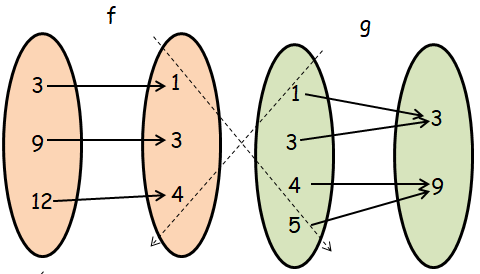
Finding composition of function f o g :

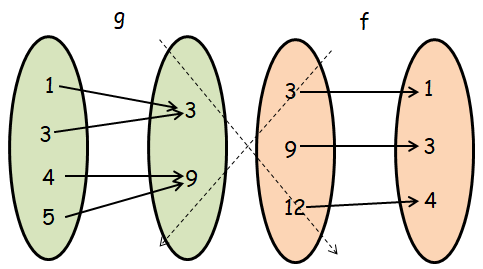
fog(x) = f[g(x)]

From g, when x = 1

• f[g(1)] = f[3] ==> 1, then (1, 1)

From g, when x = 3

• f[g(3)] = f[3] ==> 1, then (3, 1)

From g, when x = 4

• f[g(4)] = f[9] ==> 3, then (4, 3)

From g, when x = 5

• f[g(5)] = f[9] ==> 3, then (5, 3)

fog = { (1, 1), (3, 1), (4, 3), (5, 3) }

Finding composition of function g o f :

gof(x) = g[f(x)]

From f, when x = 3

• g[f(3)] = g[1] ==> 3, then (3, 3)

From f, when x = 9

• g[f(9)] = g[3] ==> 3, then (9, 3)

From f, when x = 12

• g[f(12)] = g[4] ==> 9, then (12, 9)

gof = { (3, 3) (9, 3) (12, 9) }

Problem 2 :

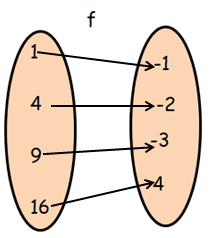
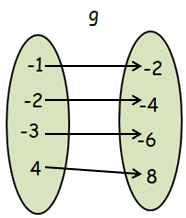
Let f = { (1, -1) (4, -2) (9, -3) (16, 4) }

and

g = { (-1, -2) (-2, -4) (-3, -6) (4, 8) }

Show that gof is defined while fog is not defined. Also find gof.

Solution :

Finding composition of function g o f :

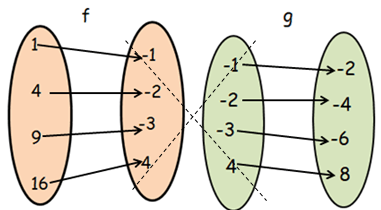
gof(x) = g[f(x)]

From f, when x = 1

• g[f(1)] = g[-1] ==> -2, then (1, -2)

From f, when x = 4

• g[f(4)] = g[-2] ==> -4, then (4, -4)

From f, when x = 9

• g[f(9)] = g[-3] ==> -6, then (9, -6)

From f, when x = 16

• g[f(16)] = g[4] ==> 8, then (16, 8)

gof = { (1, -2) (4, -4) (9, -6) (16, 8) }

Finding composition of function f o g :

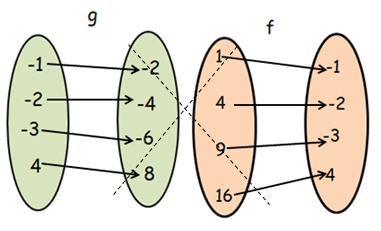
fog(x) = f[g(x)]

From g, when x = -1

• f[g(-1)] = f[-2]

There is no input -2 in the relation f. So, the function fog is not defined.

Problem 3 :

If

f = {(1,3) (2,1) (3,4) (4,2)}

and

g = {(1,2) (2,3) (3,4) (4,1)}

then find n(fog)

Solution :

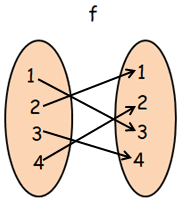
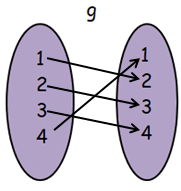
Finding composition of function f o g :

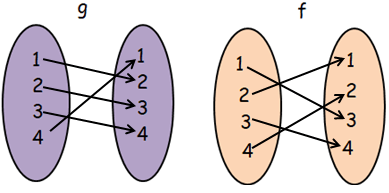
fog(x) = f[g(x)]

From g, when x = 1

• f[g(1)] = f[2] ==> 1, then (1, 1)

From g, when x = 2

• f[g(2)] = f[3] ==> 4, then (2, 4)

From g, when x = 3

• f[g(3)] = f[4] ==> 2, then (3, 2)

From g, when x = 4

• f[g(4)] = f[1] ==> 3, then (4, 3)

fog = { (1, 1), (2, 4) (3, 2) (4, 3) }

Number of ordered pairs in fog :

n[fog] = 4

Problem 4 :

If

f = {(1, 4), (2, 5), (3, 6)} and g = {(4, 8), (5, 7), (6, 9)}

then gof is

a) { }                  b) {(1,8), (2, 7), (3, 9)}

c) {(1,7), (2, 8), (3, 9)}             d) {(1,8), (2, 5), (3, 9)}

Solution :

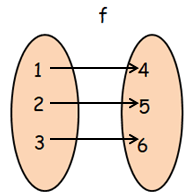
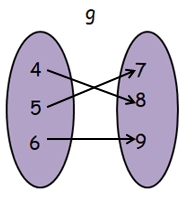
Finding composition of function g o f :

gof(x) = g[f(x)]

From f, when x = 1

• g[f(1)] = g[4] ==> 8, then (1, 8)

From f, when x = 2

• g[f(2)] = g[5] ==> 7, then (2, 7)

From f, when x = 3

• g[f(3)] = g[6] ==> 9, then (3, 9)

fog = { (1, 8), (2, 7) (3, 9) }

So, option b is correct.