HOW TO FIND FACTORS OF A NUMBER

Problem 1 :

List all the factors of :

a)  10

b)  18

c)  30

d)  44

e)  56

f)  50

g)  84

Solution :

a)

10 is divisible by the following numbers, we can write

So, the factors of 10 are 1, 2, 5 and 10.

b) 

18 is divisible by the following numbers, we can write

So, the factors of 18 are 1, 2, 3, 6, 9 and 18.

c) 

30 is divisible by the following numbers, we can write

So, the factors of 30 are 1, 2, 3, 5, 6, 10, 15, and 30.

d)

44 is divisible by the following numbers, we can write

So, the factors of 44 are 1, 2, 4, 11, 22 and 44.

e)

56 is divisible by the following numbers, we can write

So, the factors of 44 are 1, 2, 4, 7, 8, 14, 28 and 56.

f)

50 is divisible by the following numbers, we can write

So, the factors of 50 are 1, 2, 5, 10, 25 and 50.

g)

84 is divisible by the following numbers, we can write

So, the factors of 84 are 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42 and 84.

Problem 2 :

Find the prime factors of 15.

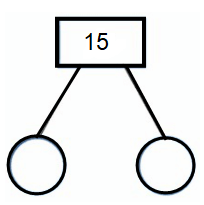
Solution :

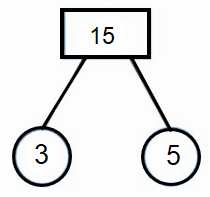
Problem 3 :

Find the prime factors of 14

Solution :

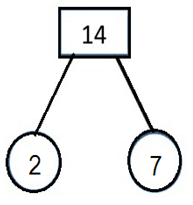
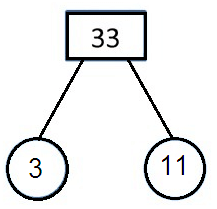
Problem 4 :

Find the prime factors of 33

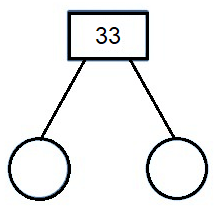
Solution :

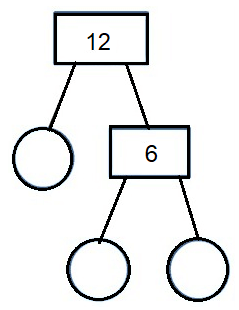
Find the missing factors of the following :

Problem 5 :

Solution :

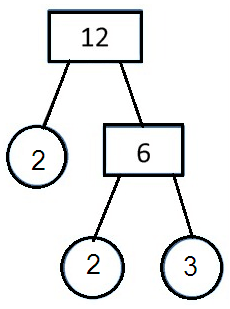
Problem 6 :

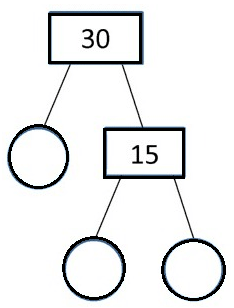
Solution :

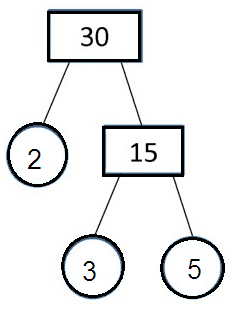
Problem 7 :

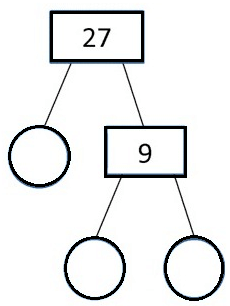
Solution :

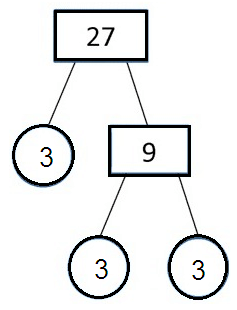
Problem 8 :

Complete the factorizations below.

a)  24 = 6 x ….

b)  25 = 5 x ….

c)  100 = 5 x ….

d)  88 = 11 x ….

Solution :

Problem 9 :

Write the largest factor other than itself, for each of the following numbers.

a)  12

b)  18

c)  27

d)  48

Solution :

a)

The factors of 12 are 1, 2, 3, 4, 6 and 12.

The largest factor of 12 is 6.

b)

The factors of 18 are 1, 2, 3, 6, 9 and 18.

The largest factor of 18 is 9.

c)

The factors of 27 are 1, 3, and 9.

The largest factor of 27 is 9.

d)

The factors of 48 are 1, 2, 3, 4, 6, 8, 12, 16, 24 and 48.

The largest factor of 48 is 24.

Problem 10 :

What is the smallest whole number which:

a)  has factors of 2, 3 and 5

b)  has factors of 3, 5 and 7

c)  has factors of 2, 3, 5 and 7

Solution :

a)

Here the given factors 2, 3 and 5 are prime factors.

=  2 × 3 × 5

=  6 × 5

=  30

So, the required smallest number is 30, which has the factors 2, 3 and 5.

b)

Here the given factors 3, 5 and 7 are prime factors.

=  3 × 5 × 7

=  15 × 7

=  105

So, the required smallest number is 105, which has the factors 3, 5 and 7.

c)

Here the given factors 2, 3, 5 and 7 are prime factors.

=  2 × 3 × 5 × 7

=  30 × 7

=  210

So, the required smallest number is 210, which has the factors 2, 3, 5 and 7.