HOW TO FIND EQUATION OF ASYMPTOTES OF HYPERBOLA

Find the coordinates of the vertices, foci and the equation of asymptotes for the hyperbola with the given equation. Then graph the hyperbola :

Problem 1 :

Solution :

The given hyperbola is symmetric about y-axis.

Here a² = 18 and b² = 20

a = 3√2 and b = 2√5

Vertices :

(0, 0)

Foci :

(c, 0) and (-c, 0) 

c² = a² + b²

c² = 18 + 20

c² = 38

c = √38

Foci are (0, √38) and (0, -√38)

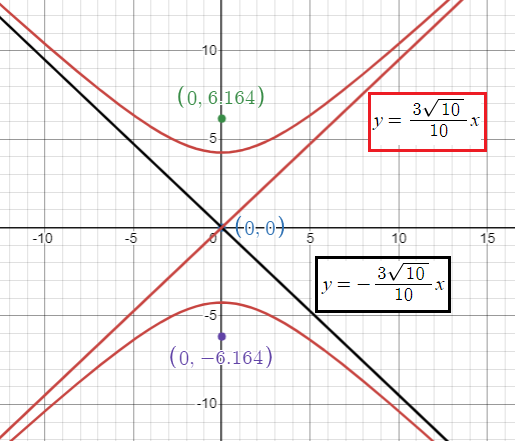
Equation of asymptotes :

y = -a/b and y = a/b

Problem 2 :

Solution :

The given hyperbola is symmetric about y-axis.

a² = 20 and b² = 25

a = 2√5 and b = 5

Vertices :

(h, k) ==> (1, -6)

Foci :

(h, k + c) and (h, k - c)

c² = a² + b²

c² = 20 + 25

c² = 45

c = 3√5

Foci are (1, -6+3√5) and (1, -6-3√5)

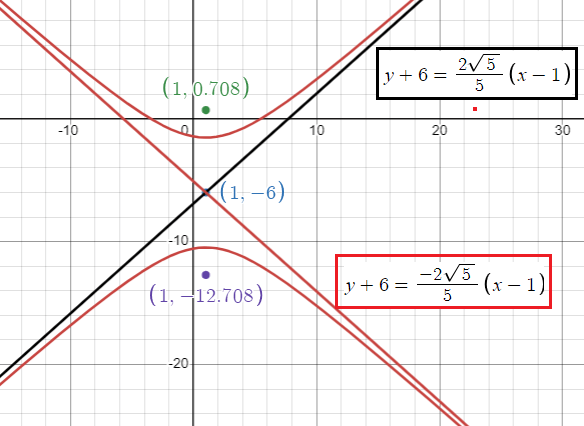
Equation of asymptotes :

Problem 3 :

x² - 36y² = 36

Solution :

Dividing by 36 on both sides

(x²/36) - (y²/1) = 1

The given hyperbola is symmetric about x-axis.

a² = 36 and b² = 1

a = 6 and b = 1

Vertices :

(h, k) ==> (0, 0)

Foci :

(h + c, k) and (h - c, k)

c² = a² + b²

c² = 36 + 1

c² = 37

c = √37

Foci are (√37, 0) and (-√37, 0)

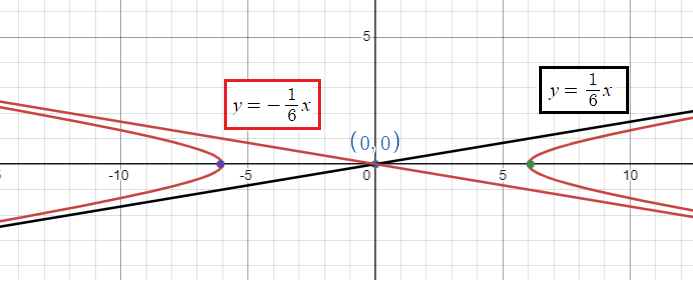
Equation of asymptotes :

Problem 4 :

5x² - 4y² - 40x - 16y  - 36 = 0

Solution :

5x² - 4y² - 40x - 16y  - 36 = 0

5x² - 40x - 4y² - 16y  - 36 = 0

5(x² - 8x) - 4(y² + 4y)  - 36 = 0

5(x² - 2⋅x⋅4 + 4² - 4²) - 4(y² + 2⋅y⋅2 + 2² - 2²)  - 36 = 0

5[(x - 4)² - 4²] - 4[(y + 2)² - 2²]  - 36 = 0

5[(x - 4)² - 16] - 4[(y + 2)² - 4]  - 36 = 0

5(x - 4)² - 80 - 4(y + 2)² + 16  - 36 = 0

5(x - 4)² - 4(y + 2)² - 80 + 16  - 36 = 0

5(x - 4)² - 4(y + 2)² - 100 = 0

5(x - 4)² - 4(y + 2)² = 100

(x - 4)² / 20 - (y + 2)² /25 = 1

The hyperbola is symmetric about x-axis.

a² = 20 and b² = 25

a = 2√5 and b = 5

Vertices :

(h, k) ==> (4, -2)

Foci :

(h + c, k) and (h - c, k)

c² = a² + b²

c² = 20 + 25

c² = 45

c = 3√5

Foci are (4+3√5, -2) and (4-3√5, -2)

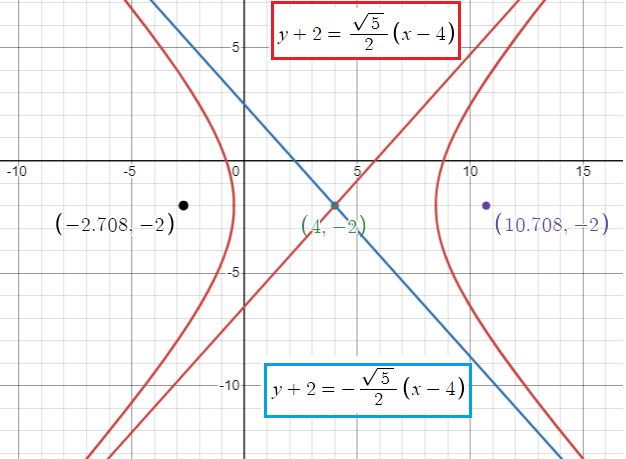
Equation of asymptotes :

Problem  5 :

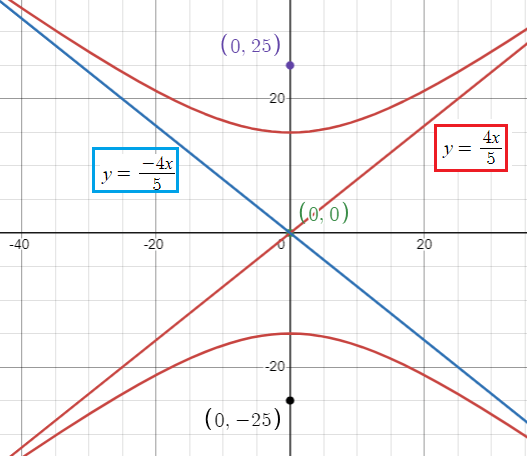
Comets that pass by Earth only once may follow hyperbolic paths. Suppose a comet's path is modeled by a branch of the hyperbola with the equation 

(y² / 225) - (x² / 400) = 1

Find the coordinates of the vertices and foci and the equation of asymptotes for the hyperbola.

Solution :

(y² / 225) - (x² / 400) = 1

The given hyperbola is symmetric about y-axis

a² = 225 and b² = 400

a = 25 and b = 20

Vertices :

(h, k) ==> (0, 0)

Foci :

(0, c) and (0, -c)

c² = a² + b²

c² = 225 + 400

c² = 625

c = 25

Foci are (0, 25) and (0, -25)

Equation of asymptotes :

y = (-b/a)x and y = (b/a)x

y = (-20/25)x, y = (20/25)x

y = -4x/5 and y = 4x/5