HOW TO FIND DISTANCE BETWEEN CHORD AND CENTER OF CIRCLE

Problem 1 :

Find x in the following giving brief reasons:

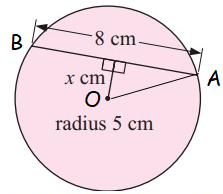
Solution:

Given, chord length = 8 cm

Half the chord = 4 cm

radius = 5 cm

Distance of a chord = x cm

By using Pythagorean Theorem,

x² + 4² = 5²

x² + 16 = 25

x² = 25 - 16

x² = 9

x = √9

x = 3 cm

So, the distance of the chord from the center is 3 cm.

Problem 2 :

Solution:

radius = 4 cm

distance from a chord = 3 cm

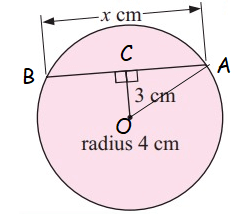
OA² = OC² + AC²

Let x = AC

4² = 3² + x²

AC = √(16 - 9)

AC = √7

Length of chord = 2√7 cm

Problem 3 :

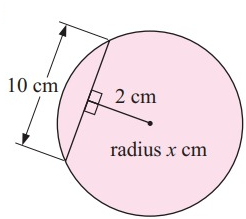
Solution:

Given, chord length = 10 cm

Half length of chord (AC) = 5 cm

radius = x cm

Distance of a chord = 2 cm

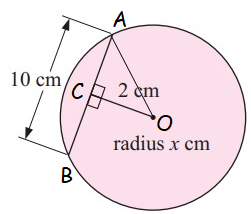
By using Pythagorean Theorem,

AC² + CO² = OA²

2² + 5² = x²

4 + 25 = x²

x² = 29

x = √29

x = 5.38 cm

Problem 4 :

A circle has a chord of length 8 cm and the shortest distance from the centre of the circle to the chord is 2 cm. Find the radius of the circle.

Solution:

Given, chord length = 8 cm

Half the chord = 4 cm

Distance of a chord = 2 cm

radius = x cm

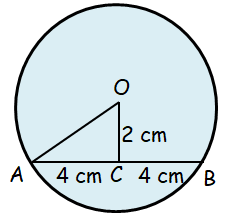
By using Pythagorean Theorem,

2² + 4² = x²

4 + 16 = x²

x² = 20

x = √20

So, the radius of the circle is 4.5 cm.

Problem 5 :

The shortest distance from the center of a circle to a chord is 2 cm. Find the length of the chord given that the radius has length 5 cm.

Solution:

Given, radius = 5 cm

distance of a chord = 2 cm

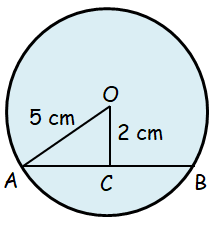
Let AC = x.

OA² = AC² + OC²

5² = x² + 2²

= √(5² - 2²)

= √(25 - 4)

= √21

2AC = AB = 2√21

So, chord length is 2√21 cm.

Problem 3 :

AD is a diameter of a circle and AB is a chord. If AD = 34 cm, AB = 30 cm, the distance of AB from the center of the circle is

a) 17 cm    b) 15 cm    c) 4 cm     d) 8 cm

Solution:

Let distance of a chord = x

Given, Diameter of the circle = AD = 34 cm

Radius of the circle = AO = 17 cm

Length of chord AB = 30 cm

Half of the chord = 15 cm

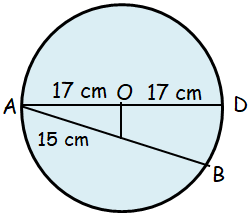
By using Pythagorean Theorem,

17² = x² + 15²

x² = 17² - 15²

x² = 289 - 225

x² = 64

x = 8

Therefore, the distance of AB from the centre of the circle is 8 cm.

So, option (d) is correct.