HOW TO FIND COTERMINAL ANGLES

Coterminal angles are angles that have the same initial side and the same terminal sides. We determine coterminal angle of a given angle by adding or subtracting 360° or  2π.

Find a positive and a negative coterminal angle for each given angle.

Problem 1 :

326°

Solution :

Drawing 326° in the xy-plane, we get

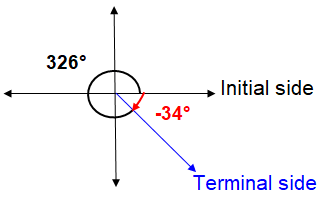
Keeping the initial side and terminal side as it is, we have to cover 34° in the negative direction (clockwise direction).

Let θ' be the coterminal angle.

θ' = 326 - 360 ==> -34°

θ' = 360 + 326 ==> 686°

So, coterminal angles of 326° are  -34° and 686°.

Note : We can find many angles like this.

Problem 2 :

530°

Solution :

Drawing 530° in the xy-plane,

360 + 170 = 530

Finding negative angle :

Keeping the initial side and terminal side as it is, we have to cover 190° in the negative direction (clockwise direction).

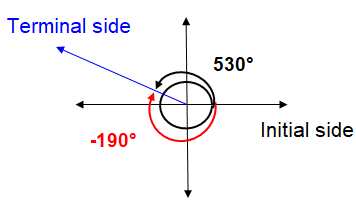
Let θ' be the coterminal angle.

θ' = 170 - 360 ==> -190°

Finding positive angle :

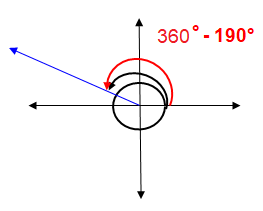
θ' = 360° - 190° ==> 170°

So, coterminal angles are -190° and 170°

Problem 3 :

-215°

Solution :

Drawing -215° in the xy-plane, the terminal side will lie in the 

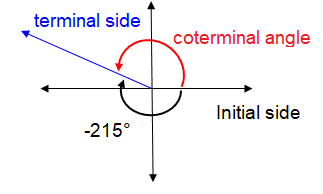
360 = -215° + (-θ')

θ' = -215° - 360°

θ' = -575°

360° - 215° ==> 145°

So, coterminal angles are -575° and 145°.

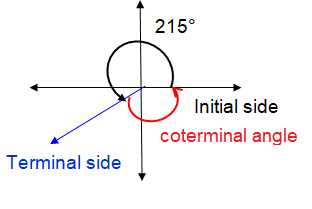
Problem 4 :

215°

Solution :

Drawing 215° in the xy-plane, the terminal side will lie in the 

Finding the positive angle :

θ' = 360° + 215° 

θ' = 575°

Finding negative angle :

In a clock wise direction, angle covered between initial side and terminal side.

θ' = 215 - 360°

θ' = -145°

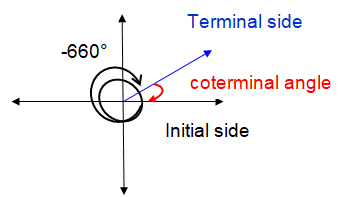
Problem 5 :

-660°

Solution :

Drawing -660° in the xy-plane,

Finding the positive angle :

Leaving the initial and terminal side as it is, we move in anticlock wise direction to cover 60°.

Finding negative angle :

Moving in a clockwise direction, we get -300°

So, the coterminal angles of  -660° are 60° and -300°.

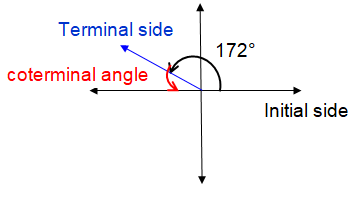
Problem 6 :

172°

Solution :

Drawing 172° in the xy-plane,

Finding the positive angle :

Leaving the initial and terminal side as it is, we move in anticlock wise direction, then we will complete a circle and reaches the same.

So, 

θ' = 360° + 172°

θ' = 532°

Finding negative angle :

Moving in a clockwise direction, 

θ' = 172° - 360°

θ' = -188°

So, the coterminal angles of  172° are 532° and -188°.

Problem 7 :

-340°

Solution :

Finding the positive angle :

Leaving the initial and terminal side as it is, we move in anticlock wise direction, we have to reach the same.

So, 

θ' = 20

Finding negative angle :

Moving in a clockwise direction, after completing the circle, keep on moving to reach the same position

θ' = - 360° - 340°

θ' = -700°

So, the coterminal angles of  -340° are 20° and -700°.

Problem 8 :

495°

Solution :

495° = 360° + 135°

Finding the positive angle :

Moving in a anticlock wise Angle between the initial side and terminal side by leaving a round, we get

θ' = 360° + 135°

θ' = 135°

Finding negative angle :

Moving in a clockwise direction, after completing the circle, keep on moving to reach the same position

θ' = 135° - 360°

θ' = -225°

So, the coterminal angles of  495° are 135° and -225°.

Problem 9 :

-210°

Solution :

Finding the positive angle :

Angle between the initial side and terminal side in anticlock wise direction 

θ' = -210° + 360°

θ' = 150°

Finding negative angle :

Moving in a clockwise direction, after completing the circle, keep on moving to reach the same position

θ' = -360° - 210°

θ' = -570°

So, the coterminal angles of  -210° are 150° and -570°.

Problem 10 :

530°

Solution :

530° = 360° + 170°

Finding the positive angle :

After completing a round angle between the initial side and terminal side is 170°.

Finding negative angle :

In a clock wise direction,

θ'  = 170° - 360°

θ' = -190°

So, the coterminal angles of  530° are 170° and  -190°.

Problem 11 :

-84°

Solution :

Finding negative angle :

In a clock wise direction,

θ'  = -360° - 84°

θ' = -444°

Finding the positive angle :

Angle between the initial side and terminal side in anticlockwise direction.

θ'  = 360° - 84°

θ'  = 276° 

So, the coterminal angles of -84° are 276° and  -444°.