HOW TO FIND CHARACTERISTICS OF GRAPHS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Domain :
How the graph is spread on the x-axis is domain. In other words, for the set of x values for which it is spreading horizontally, that is known as domain.
Range :
How the graph is spread on the y-axis is range. In other words, for the set of y-values for which it is spreading vertically, that is known as range.
Maximum or minimum :
The point where the graph reaches its maximum height is maximum. When the curve changes its direction from increasing to decreasing, there will be a maximum point.
The point where the graph reaches its minimum height is minimum. When the curve changes its direction from decreasing to increasing, there will be a minimum point.
x and y intercepts :
The curve where it cuts the x-axis is known as x-intercept, the curve where it cuts the y-axis is known as y-intercept.
How to check if it is discreate or continuous ?
Discrete functions have scatter plots as graphs and continuous functions have lines or curves as graphs.
Problem 1 :
Use the graphs to state the various features.
|
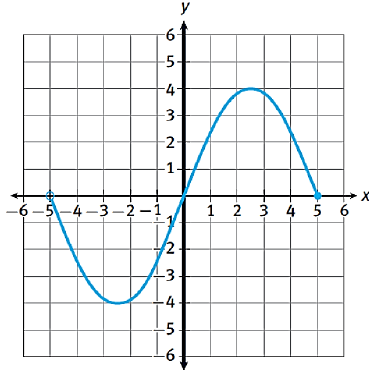
i) Domain ii) Range iii) Maximum iv) Minimum |
v) Discrete or Continuous? vi) y – intercept: vii) x – intercept: viii) 7𝑓(5)= |
Solution :
|
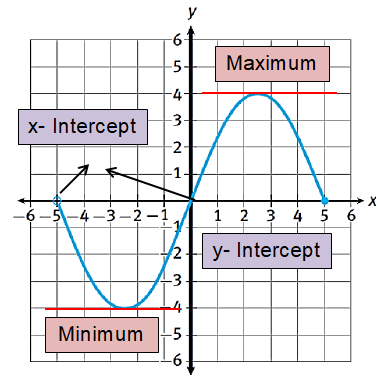
i) Domain: (-5, 5] ii) Range : [-4, 4] iii) Maximum: y = 4 iv) Minimum: y = -4 |
v) Discrete or Continuous? Continuous vi) y – intercept: y = 0 vii) x – intercept: x = 0 and x = 5 viii) 7 𝑓(5) = 0 |
Problem 2 :
|
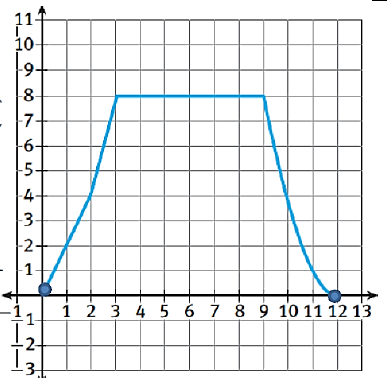
i) Domain: ii) Range: iii) Maximum: iv) Minimum: |
v) Interval of Increase: vi) Interval of Decrease: vii) 𝑓(2) + 𝑓(9) = |
Solution :
i) Domain : [0, 12]
ii) Range: [0, 8]
iii) Maximum: y = 8
iv) Minimum: y = 0
v) Interval of Increase: (0, 3)
vi) Interval of Decrease: (9, 12)
vii) 𝑓(2) = 4 and 𝑓(9) = 8
f(2) + f(9) = 4 + 8 ==> 12
Problem 3 :
|
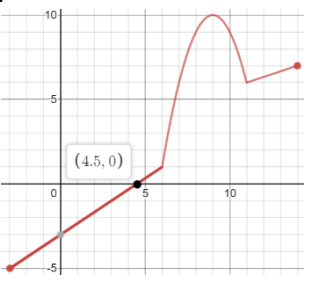
i) Domain ii) Increasing iii) Range iv) Decreasing v) x-intercept (s) |
vi) Positive vii) y-intercept viii) Negative ix) Maximum x) Minimum xi) End behaviour |
Solution :
|
Domain Increasing Range Decreasing x-intercept(s) Positive y-intercept Negative Maximum Minimum |
[-3, 14] (-3, 9) ꓴ (11, 14) [-5, 10] (9,14) (4.5,0) (4.5,14] (0,-3) [-3,4.5) (9,10) (-3,-5) |
End Behavior: 𝑎𝑠 x → −3, y → −5; 𝑎𝑠 x → 14, y → 10
Problem 4 :
|
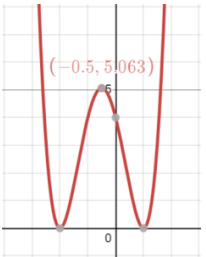
i) Domain ii) Range iii) x-intercept(s) iv) y-intercept v) Maximum |
vi) Increasing vii) Decreasing viii) Positive ix) Negative x) Minimum xi) End behaviors |
Solution :
|
Domain Increasing Range Decreasing x-intercept(s) Positive y-intercept Negative Maximum Minimum End Behavior |
(-∞, ∞) (-2,-0.5) ꓴ (1, ∞) (0, ∞) (-∞,-2) ꓴ (-0.5,1) (-2,0) & (1,0) (-∞,-2) ꓴ (-2,1) ꓴ(1, ∞) (0,4) none (-0.5,5.063) (-2,0) & (1,0) x → −∞, y → +∞; 𝑎𝑠 x → +∞, y → +∞ |
Problem 5 :
|
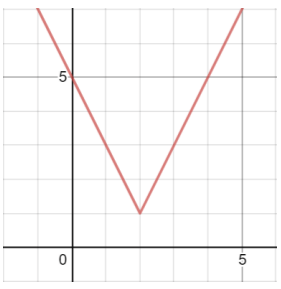
i) Domain ii) Increasing iii) Range iv) Decreasing v) x-intercept(s) |
vi) Positive vii) y-intercept viii) Maximum ix) Minimum x) End behavior |
Solution :
|
i) Domain ii) Increasing iii) Range iv) Decreasing v) x-intercept(s) vi) Positive vii) y-intercept viii) Maximum ix) Minimum x) End behavior |
(-∞, ∞) (2, ∞) (1, ∞) (-∞,2) none (-∞, ∞) (0,5) none (2,1) x → −∞, y → +∞; 𝑎𝑠 x → +∞, y → +∞ |
Problem 6 :
For each polynomial function, identify the following characteristics.
a) The type of function whether it is even or odd degree.
b) The end behavior of the graph of the function
c) the number of possible x-intercepts.
d) where the graph has a maximum or minimum value
e) the y-intercept.
Then, match each function to its corresponding graph.
i) f(x) = 2x3 - 4x2 + x + 2
ii) f(x) = -x4 + 10x2 + 5x - 6
iii) f(x) = -2x5 + 5x3 - x + 1
iv) f(x) = x4 - 5x3 + 16
Solution :
i) f(x) = 2x3 - 4x2 + x + 2
a) Degree of the polynomial = Odd degree polynomial
b) Sign of leading coefficient = positive
when,
lim x--> ∞, f(X) --> ∞
lim x--> -∞, f(X) --> -∞
c) The number of possible x-intercepts are 3.
d) Using rational root theorem,
Factors of constant p = ±1, ±2
Factors of Leading coefficient q = ±1, ±2
p/q = ±1, ±1/2, ±2
e) y-intercept :
Put x = 0
f(0) = 2(0)3 - 4(0)2 + 0 + 2
= 2
By analyzing the end behavior, rational roots and y-intercept. It is clear that option D is correct.
ii) f(x) = -x4 + 10x2 + 5x - 6
a) Degree of the polynomial = even degree polynomial
b) Sign of leading coefficient = negative
when,
lim x--> ∞, f(X) --> -∞
lim x--> -∞, f(X) --> -∞
c) The number of possible x-intercepts are 4.
d) Using rational root theorem,
Factors of constant p = ±1, ±2, ±3, ±6
Factors of Leading coefficient q = ±1
p/q = ±1, ±2, ±3, ±6
e) y-intercept :
Put x = 0
f(0) = -(0)4 + 10(0)2 + 5(0) - 6
= -6
By analyzing the end behavior, rational roots and y-intercept. It is clear that option B is correct.
iii) f(x) = -2x5 + 5x3 - x + 1
a) Degree of the polynomial = odd degree polynomial
b) Sign of leading coefficient = negative
when,
lim x--> ∞, f(X) --> -∞
lim x--> -∞, f(X) --> ∞
c) The number of possible x-intercepts are 5.
d) Using rational root theorem,
Factors of constant p = ±1
Factors of Leading coefficient q = ±1, ±2
p/q = ±1, ±1/2
e) y-intercept :
Put x = 0
f(0) = -2(0)5 + 5(0)3 - 0 + 1
= 1
By analyzing the end behavior, rational roots and y-intercept. It is clear that option A is correct.
iv) f(x) = x4 - 5x3 + 16
a) Degree of the polynomial = even degree polynomial
b) Sign of leading coefficient = positive
when,
lim x--> ∞, f(X) --> ∞
lim x--> -∞, f(X) --> ∞
c) The number of possible x-intercepts are 4.
d) Using rational root theorem,
Factors of constant p = ±1, ±2, ±4, ±8, ±16
Factors of Leading coefficient q = ±1
p/q = ±1, ±2, ±4, ±8, ±16
e) y-intercept :
Put x = 0
f(0) = 04 - 5(0)3 + 16
= 16
By analyzing the end behavior, rational roots and y-intercept. It is clear that option C is correct.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling