HOW TO FIND AVERAGE RATE OF CHANGE OVER AN INTERVAL FROM A GRAPH

Use the following graph to find the average rate of change of the given interval.

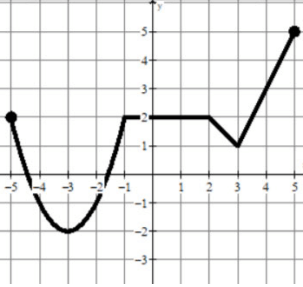
Problem 1 :

Find the average rate of change in the interval

-5 ≤ x ≤ -2

Solution :

Let a = -5 and b = -2

• Tracing the curve at x = -5, we get one of the point on the curve (-5, 2).
• Tracing the curve at x = -2, we get one of the point on the curve (-2, -1).

f(a) = f(-5) = 2 and f(b) = f(-2) = -1

Problem 2 :

Find the average rate of change in the interval

[-1, 5]

Solution :

Let a = -1 and b = 5

• Tracing the curve at x = -1, we get one of the point on the curve (-1, 2).
• Tracing the curve at x = 5, we get one of the point on the curve (5, 5).

f(a) = f(-1) = 2 and f(b) = f(5) = 5

Problem 3 :

Find the average rate of change in the interval

-4 ≤ x ≤ -2

Solution :

Let a = -4 and b = -2

• Tracing the curve at x = -4, we get one of the point on the curve (-4, -1).
• Tracing the curve at x = -2, we get one of the point on the curve (-2, -1).

f(a) = f(-4) = -1 and f(b) = f(-2) = -1

Problem 4 :

Regarding the graph at the right, what is the average rate of change over the interval -1 < x < 5 ?

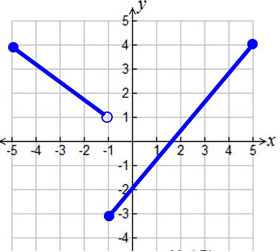
Solution :

Let a = -1, b = 5

f(a) = f(-1) = -3 and f(b) = f(5) = 4

Problem 5 :

Find the average rate of change between x = 0 and x = 4

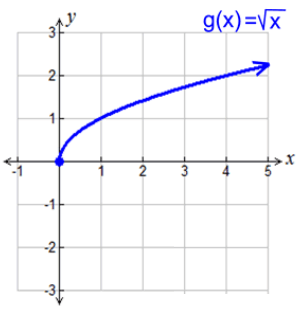
Solution :

Let a = 0, b = 4

f(a) = f(0) = √0 = 0

 and

 f(b) = f(4) = √4 = 2