How to Find Area of Regular Polygon With Side Length
What is polygon ?
A polygon can be defined as a flat or plane, two-dimensional closed shape with straight sides. It does not have curved sides.
Regular polygon :
A polygon having equal sides and equal angles is a regular polygon.
To find area of regular polygon, we use the formula
What is Apothem ?
A line from the center of a regular polygon at right angles to any of its sides.
Problem 1 :
What is the area of regular nanagon with 10 cm sides.
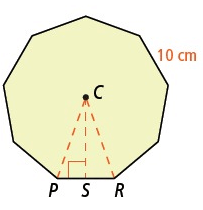
Solution :
Number of sides of Nanagon = 9
∠PCR = 360/9 ==> 40
Drawing perpendicular bisector CS, we get
∠PCS = 40/2 ==> 20 and PS = PR/2 ==> 5 cm
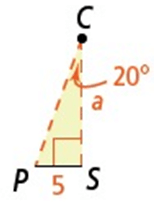 |
tan 20˚ = 5/a a = 5/tan 20˚ A = 1/2ap = 1/2 ∙ 5/tan 20˚ ∙ 90 ≈ 618.1824194 |
The area of the regular nonagon is about 618 cm².
Problem 2 :
Octagon with side length 6 cm
Solution :
Number of sides = 8
∠AOB = 360/8 ==> 45
∠COB = 45/2 ==> 22.5
Side length = 6 cm
Length of an apothem,
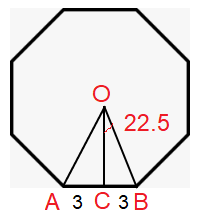 |
OC = Apothem tan θ = BC/OC tan 22.5 = 3/a a = 3 / tan 22.5 a = 3/0.414 a = 7.246 |
Perimeter = sides × length
= 8 × 6
P = 48 cm
Area = 1/2 × aP
= 1/2 × 7.246 × 48
A = 173.91 cm²
The area of the regular octagon is about 174 cm².
Problem 3 :
Decagon with side length 4 yd
Solution :
Number of sides = 10
Side length = 4 yd
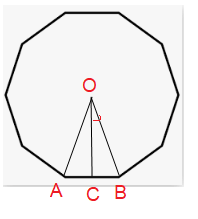
Length of an apothem,
AC = 2, BC = 2, Apothem = OC
∠AOB = 360/10 ==> 36
∠COB = 36/2 ==> 18
OC = Apothem
tan θ = BC/OC
tan 18 = 2/a
a = 2 / tan 18
a = 2/0.325
a = 6.153
Perimeter = sides × length
= 10 × 4
P = 40 yd
Area = 1/2 × aP
= 1/2 × 6.153 × 40
A = 123.06 yd²
The area of the regular decagon is about 123 yd².
Problem 4 :
The Pentagon in Arlington, Virginia, is one of the world’s largest office buildings. It is a regular pentagon, and the length of each of its sides is 921 ft. what is the area of land that the Pentagon covers to the nearest thousand square feet?
Solution :
Number of sides = 5
Side length = 921 ft
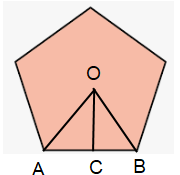
∠AOB = 360/5 ==> 72
∠COB = 72/2 ==> 36
Length of an apothem,
tan θ = BC/OC
tan 36 = 921/a
a = 921/1.452
a = 634.3
Perimeter = sides × length
= 5 × 921
P = 4605 ft
Area = 1/2 × aP
= 1/2 × 634.3 × 4605
A = 1460475.75 ft²
The area of the regular pentagon is about 1460475 ft².
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling