HOW TO FIND AREA OF REGULAR POLYGON WITH RADIUS
Radius is the distance between center and one of the vertex.
Area of regular polygon = 1/2 x Perimeter x Apothem
Perimeter = Sum of length of all sides
Apothem is the perpendicular distance between center and one of the sides.
Find the area of each polygon with given radius. Leave the answer in radical.
Problem 1 :
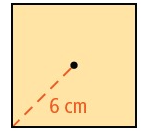
Solution :
Number of sides of the polygon = 4
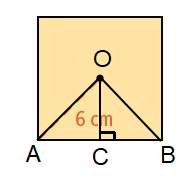
∠AOB = 360/4 ==> 90
∠COB = 90/2 ==> 45
OB = Radius = 6 cm
In triangle COB,
|
sin θ = BC / OB sin 45 = BC / 6 1/√2 = BC / 6 BC = 6/√2 BC = 3√2 |
tan θ = BC / OC tan 45 = 3√2 / OC 1 = 3√2 / OC OC = 3√2 |
AB = 2 BC ==> 2(3√2) ==> 6√2
Area of regular polygon = 1/2 x Perimeter x Apothem
Perimeter = 4 (6√2) ==> 24√2
Area of polygon = (1/2) x 24√2 x 3√2
= 72 cm2
Problem 2 :
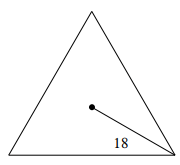
Solution :
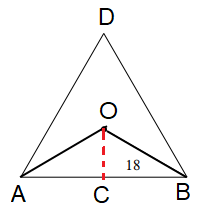
Number of sides of the polygon = 3
radius = 18
∠AOB = 360/3 ==> 120
∠COB = 120/2 ==> 60
OB = 18 (radius)
In triangle OCB,
|
sin θ = BC / OB sin 60 = BC / 18 √3/2 = BC / 18 BC = 9√3 |
tan θ = BC / OC tan 60 = 9√3 / OC √3 = 9√3 / OC OC = 9 Apothem = 9 |
AB = 2(9√3) ==> 18√3
Area of regular polygon = 1/2 x Perimeter x Apothem
Perimeter = 3(18√3) ==> 54√3
Area of regular polygon = 1/2 x 54√3 x 9
= 243√3
Problem 3 :
Solution :
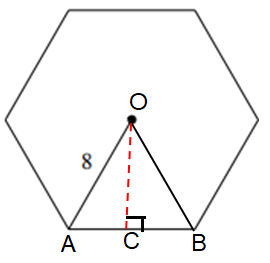
Number of sides of the polygon = 6
radius = 8
∠AOB = 360/6 ==> 60
∠COB = 60/2 ==> 30
OB = 8 (radius)
In triangle OCB,
|
sin θ = BC / OB sin 30 = BC / 8 1/2 = BC / 8 BC = 4 |
tan θ = BC / OC tan 30 = 4 / OC 1/√3 = 4 / OC OC = 4√3 Apothem = 4√3 |
AB = 2(4) ==> 8
Area of regular polygon = 1/2 x Perimeter x Apothem
Perimeter = 6(8) ==> 48
Area of regular polygon = 1/2 x 48 x 4√3
= 96√3
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling