HOW TO FIND AREA AND PERIMETER OF SIMILAR FIGURES

Problem 1 :

Triangle HIJ is similar to triangle STR, what is the perimeter of triangle STR

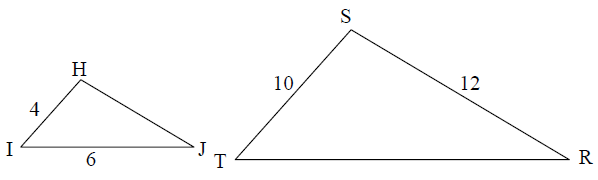
Solution :

Since the given sides are similar,

• HI and ST are corresponding sides.
• IJ and TR are corresponding sides.
• HJ and SR are corresponding sides.

HI : ST = 4 : 10

HI : ST = 2 : 5

Perimeter of STR :

= ST + TR + SR

= 10 + 15 + 12

= 37

Problem 2 :

If the two triangles are similar

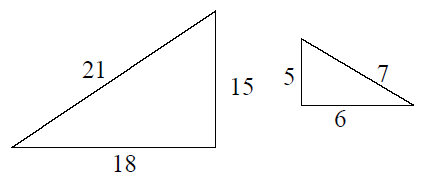
Find

i) Scale factor

ii) Ratio of perimeter

iii)  Ratio of area

Solution :

The sides which are having side lengths 21 and 7, they are corresponding sides.

The sides lengths 15 and 5 are corresponding, then 18 and 6 are corresponding.

Ratio = 21 : 7 ==> 3 : 1

i) Scale factor = 3 : 1

ii)  Ratio of perimeter = 3 : 1

iii)  Ratio of area = 3² : 1²

Problem 3 :

Two triangles have a scale factor of 2/3. The area of the larger triangle is 12 cm². What is the area of smaller triangle.

Solution :

Area of smaller triangle / Area of larger triangle = (2/3)²

Area of larger triangle = 12 cm²

Area of smaller triangle / 12 = (2/3)²

Area of smaller triangle = 12 (4/9)

Area of smaller triangle = 5.3 cm²

Problem 4 :

If the length of each side of triangle is cut to 1/3 of its original size, what happens to the area of the triangle ?

The new area is _______________ of the original area.

Solution :

From the given information, every side is being divided into 1/3 of the original size. So, the ratio is 1 : 3.

Relationship between scale factor and area :

Area of smaller triangle : Area of larger triangle = (1 : 3)²

Area of smaller triangle : Area of larger triangle = 1 : 9

Area of smaller triangle = (1/9) of area of larger triangle.

Problem 5 :

For the two triangles below to be similar, which of the following be true ?

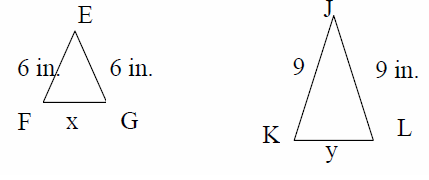
a)  x = 2y/3    b)  c = 3y/2     c)  x = 3y     d)  x = y

Solution :

Since the given shapes are similar,

EF : KJ ==> 6 : 9 ==> 2 : 3

FG : KL ==> x : y

x : y = 2 : 3

x/y = 2/3

x = 2y/3

Problem 6 :

An architect is building a model of a tennis court for a new client. On the model, the court is 6 inches wide and 13 inches long. An official tennis court is 36 feet wide. What is the length of a tennis court ?

Solution :

Let x be the length of tennis court.

Since the shapes are similar, the ratio between model to official tennis court is 

6 : 13 = 36 : x

6/13 = 36/x

6x = 36(13)

x = 36(13)/6

x = 6 (13)

x = 78

So, length of official tennis court is 78 feet.