HOW TO FIND AMPLITUDE AND PERIOD OF SINE AND COSINE FUNCTIONS

A periodic function is one which repeats itself over and over in horizontal direction.

What is period ?

The period of a periodic function is the length of one repetition or cycle

What is amplitude ?

The amplitude is the vertical distance between a maximum point and the principal axis.

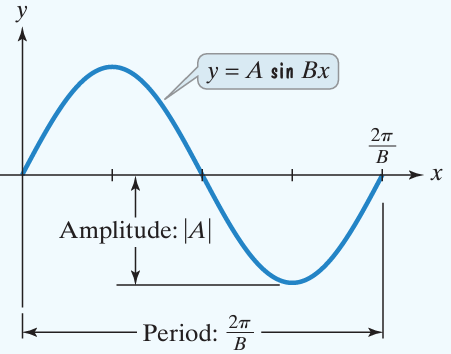
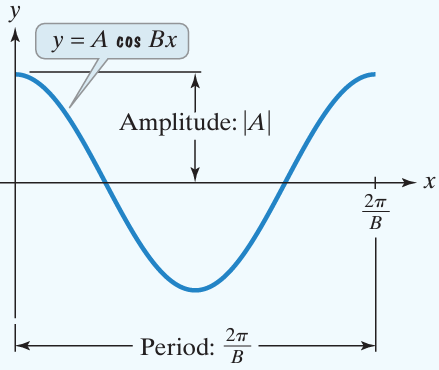
• The amplitude is |A|
• Period is 2π/B, for B > 0

For the following sine and cosine functions find 

i) amplitude 

ii) period

Problem 1 :

f(x) = sin 4x

Solution :

f(x) = sin 4x

Amplitude (A) = 1, B = 4, period = 2π/4 ==> π/2

Problem 2 :

f(x) = cos 5x

Solution :

f(x) = cos 5x

Amplitude (A) = 1, B = 5, period = 2π/5

Problem 3 :

f(x) = sin x

Solution :

f(x) = sin x

Amplitude (A) = 1, B = 1, period = 2π/1 ==> π

Problem 4 :

f(x) = 4 cos x

Solution :

f(x) = 4 cos x

Amplitude (A) = 4, B = 1, period = 2π/1 ==> 2π

Problem 5 :

f(x) = -2 sin x

Solution :

f(x) = -2 sin x

Amplitude (A) = 2, B = 1, period = 2π/1 ==> 2π

Problem 6 :

f(x) = 2 sin (4x)

Solution :

f(x) = 2 sin (4x)

Amplitude (A) = 2, B = 4, period = 2π/4 ==> π/2

Problem 7 :

f(x) = 3 sin (2/3) x

Solution :

f(x) = 3 sin (2/3) x

Amplitude (A) = 3, B = 2/3, period = 2π/(2/3) ==> 3π

Problem 8 :

f(x) = -4 cos 5x

Solution :

f(x) = -4 cos 5x

Amplitude (A) = 4, B = 5, period = 2π/5

Problem 9 :

f(x) = 3 cos 2x

Solution :

f(x) = 3 cos 2x

Amplitude (A) = 3, B = 2, period = 2π/2 ==>π

Problem 10 :

f(x) = sin 2x

Solution :

f(x) = sin 2x

Amplitude (A) = 1, B = 2, period = 2π/2 ==>π

Problem 11 :

f(x) = sin (x/3)

Solution :

f(x) = sin (x/3)

Amplitude (A) = 1, B = 1/3, period = 2π/(1/3) ==> 6π

Problem 12 :

f(x) = sin 0.6x

Solution :

f(x) = sin (0.6x)

Amplitude (A) = 1, B = 0.6, period = 2π/0.6

= 2π/(6/10)

= 20π/6

= 10π/3

Problem 13 :

f(x) = sin 4x + 1

Solution :

f(x) = sin (4x) + 1

Amplitude (A) = 1, B = 4, period = 2π/4

= π/2