HOW TO FIND A POINT OF DISCONTINUITY OF RATIONAL FUNCTION

We say a function is continuous if its domain is an interval, and it is continuous at every point of that interval.

A point of discontinuity is the only bad point for the function on some interval.

How to find point of discontinuity of a rational function ?

The discontinuities of a rational function can be found by setting its denominator equal to zero and solving it.

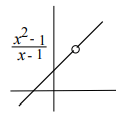
The function given above is not continuous at x = 1

Types of discontinuity :

(i) Removable

(ii) Jump

(iii)  Essential

(iv) Infinite

Find any points of discontinuity for each rational function.

Problem 1 :

y = (x + 3)/(x – 4) (x + 3)

Solution :

To find points of discontinuity, let us equate the denominators to 0.

y = (x + 3)/(x – 4) (x + 3)

x – 4 = 0

x = 4

x + 3 = 0

x = -3

The function is discontinuous at x = -3 and 4.

Problem 2 :

y = (x - 2)/(x² – 4)

Solution :

To find point of discontinuity, let us equate the denominator to 0.

y = (x - 2)/(x² – 4)

x² – 4 = 0

x² = 4

x = ±2

The function is discontinuous at x = ±2.

Problem 3 :

y = (x - 3) (x + 1)/(x – 2)

Solution :

To find point of discontinuity, let us equate the denominator to 0.

y = (x - 3) (x + 1)/(x – 2)

x – 2 = 0

x = 2

The function is discontinuous at x = 2.

Problem 4 :

y = 3x(x + 2)/x(x + 2)

Solution :

To find point of discontinuity, let us equate the denominator to 0.

y = 3x(x + 2)/x(x + 2)

x(x + 2) = 0

x = 0, x + 2 = 0

x = 0 and x = -2

The function is discontinuous at x = 0, -2.

Problem 5 :

y = 2/(x + 1)

Solution :

To find point of discontinuity, let us equate the denominator to 0.

y = 2/(x + 1)

x + 1 = 0

x = -1

The function is discontinuous at x = -1.

Problem 6 :

y = 4x/(x³ – 9x)

Solution :

To find point of discontinuity, let us equate the denominator to 0.

y = 4x/(x³ – 9x)

x³ – 9x = 0

x(x² - 9) = 0

Equating each factor to zero, we get

x = 0, x² - 9 = 0

x=  0 and x = ±3

The function is discontinuous at x = 0, ±3.