HOW TO EVALUATE COMPOSITION OF FUNCTION FROM GRAPH
To evaluate composition of functions, we have to use the following procedure :
Step 1 :
In (f ∘ g)(x),
(f ∘ g)(x) = f [g(x)]
Here x is the input for the function g and g(x) is the input for the function f.
Step 2 :
For the particular value x, draw the vertical line through this point. The vertical line will intersect the graph at certain point.
That is the output.
Step 3 :
Now this output will act as input for the function f. Draw the vertical line through this point, the vertical line will intersect the graph f at a certain point. That is the required result for the composition of function.
Problem 1 :
The first of the two graphs shows two functions 𝑓 𝑎𝑛𝑑 𝑔. The second shows two functions ℎ 𝑎𝑛𝑑 𝑘. Use the graphs to compute the following:
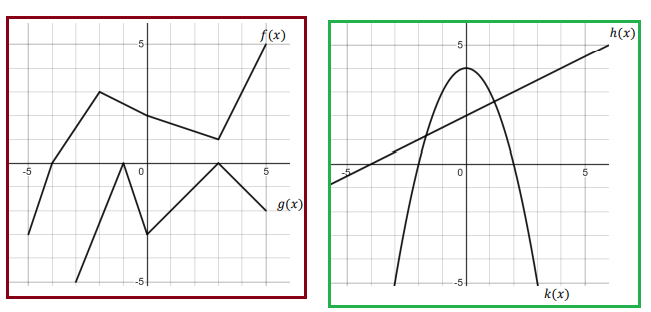
|
1) (𝑔 ◦ 𝑓)(−4) = 2) (𝑓 ◦ 𝑔)(3) = 3) (𝑓 ◦ 𝑓)(−2) = 4) (𝑔 ◦ 𝑔)(3) = 5) (𝑔 ◦ 𝑓)(−5) = 6) (𝑔 ◦ 𝑓)(−3) = 7) (ℎ ◦ 𝑘)(0) = |
8) (ℎ ◦ 𝑘)(−1) = 9) (ℎ ◦ 𝑘)(2) = 10) (ℎ ◦ 𝑘)(−3) = 11) (𝑘 ◦ ℎ)(0) = 12) (𝑘 ◦ ℎ)(2) = 13) (𝑘 ◦ ℎ)(−4) = 14) (𝑘 ◦ ℎ)(−2) = |
Solution :
1) (𝑔 ◦ 𝑓)(−4) = g[f(-4)]
To get the value of f(-4), we have to draw the vertical line through x = -4.
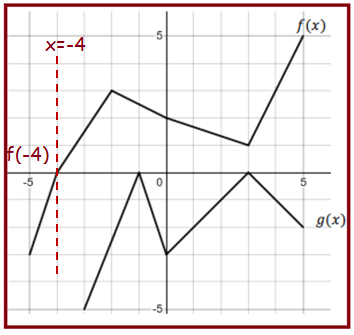
The vertical line is intersecting the graph f at 0. So, the value of f(-4) is 0.
(𝑔 ◦ 𝑓)(−4) = g[0]
Now, we have to observe the point of intersection of the vertical line drawn at x = 0 to the function g. At -3, the vertical line is intersecting the graph g. So,
(𝑔 ◦ 𝑓)(−4) = -3
2) (𝑓 ◦ 𝑔)(3) = f[g(3)] = f[0] ==> 2
3) (𝑓 ◦ 𝑓)(−2) = f[f(-2)] = f[3] ==> 1
4) (𝑔 ◦ 𝑔)(3) = g[g(3)] = g[0] ==> -3
5) (𝑔 ◦ 𝑓)(−5) = g[f(-5)] = g[-3] ==> -5
6) (𝑔 ◦ 𝑓)(−3) = g[f(-3)] = g[1.5] ==> -1.5
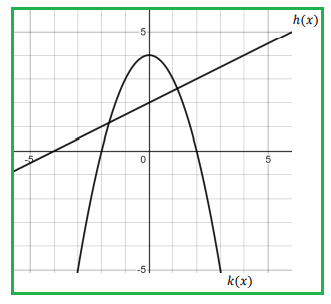
7) (ℎ ◦ 𝑘)(0) = h[k(0)] = h[4] ==> 4
8) (ℎ ◦ 𝑘)(−1) = h[k(-1)] = h[3] ==> 3.5
9) (ℎ ◦ 𝑘)(2) = h[k(2)] = h[0] ==> 2
10) (ℎ ◦ 𝑘)(−3) = h[k(-3)] = h[-5] ==> -0.5
11) (𝑘 ◦ ℎ)(0) = k[h(0)] = k[2] ==> 0
12) (𝑘 ◦ ℎ)(2) = k[h(2)] = k[3] ==> -5
13) (𝑘 ◦ ℎ)(−4) = k[h(-4)] = k[0] ==> 4
14) (𝑘 ◦ ℎ)(−2) = k[h(-2)] = k[1] ==> 3
Problem 2 :
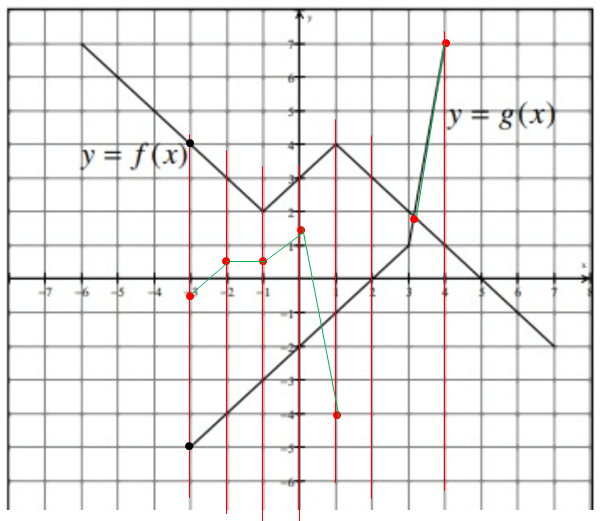
Refer to the graph to complete the statements below.
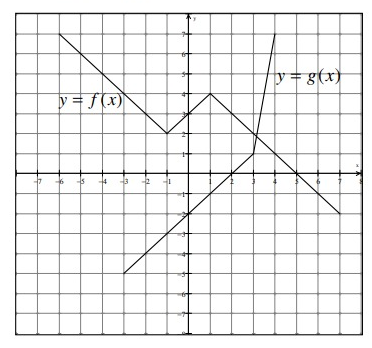
a) (f + g)(-3) = ______
b) (f · g)(2) = ______
c) (f/g)(-1) = ______
d) (f ∘ g)(3) = ______
e) g-1(-4) = ______
f) Evaluate (f ∘ f)(2) ______
g) Evaluate g(f(g(1))) ______
h) State the domain of f + g _____
i) State the domain of f/g. ______
j) Evaluate (f(3))3 - 4g(-2) ______
k) For what value(s) is f(x) = 3? _______
Solution:
a) (f + g)(-3)
(f + g)(-3) = f(-3) + g(-3)
To evaluate f(-3) and g(-3), we have to draw the vertical lines at x = -3. The line is intersecting the curve f(x) and g(x) at 4 and -5 respectively.
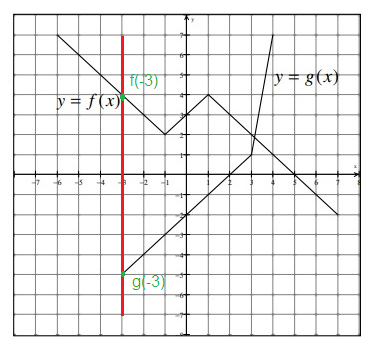
(f + g)(-3) = f(-3) + g(-3)
= 4 + (- 5)
(f + g)(-3) = -1
b) (f · g)(2)
(f · g)(2) = f(2) · g(2)
To evaluate f(2) and g(2), we have to draw the vertical lines at x = 2. The line is intersecting the curve f(x) and g(x) at 3 and 0 respectively.
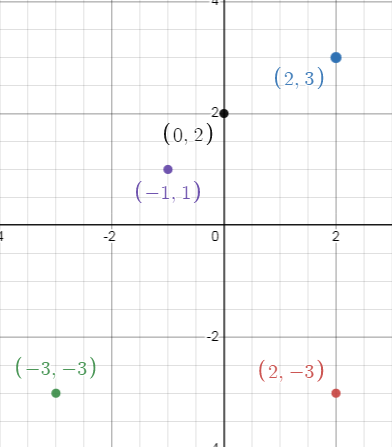
(f · g)(2) = f(2) · g(2)
= 3 · 0
(f · g)(2) = 0
c) (f/g)(-1)
(f/g)(-1) = f(-1) / g(-1)
To evaluate f(-1) and g(-1), we have to draw the vertical lines at x = -1. The line is intersecting the curve f(x) and g(x) at 2 and -3 respectively.
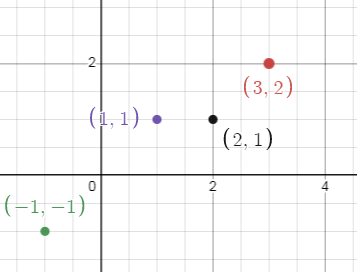
(f/g)(-1) = f(-1) / g(-1)
(f/g)(-1) = 2/(-3)
d) (f ∘ g)(3)
(f ∘ g)(3) = f [g(3)]
= f [1]
(f ∘ g)(3) = 4
e) g-1(-4)
f(x) = y, then f-1(y) = x
Let g-1(-4) = x
-4 = g(x)
for what value of x, the value of y will be -4. So x = -3.
f) (f ∘ f)(2)
(f ∘ f)(2) = f [f(2)]
= f [3]
(f ∘ f)(2) = 2
g) g(f(g(1)))
g(f(g(1))) = f [g(1)]
= g [f (-1)]
= g(2)
= 0
h) State the domain of f + g _____
Domain of f(x) = [-6, 7]
Domain of g(x) = [-3, 4]
[-6, 7] n [-3, 4] = [-3, 4]
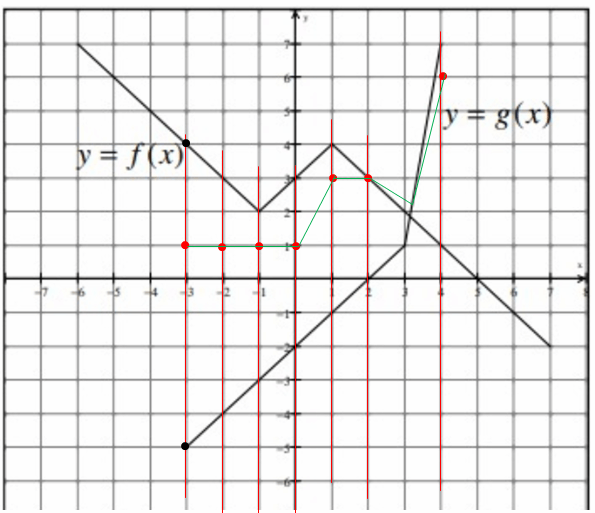
[-6, 7] n [-3, 4] = [-3, 4]
So, the domain of (f + g)(x) is [-3, 4].
i) State the domain of f/g. ______
From the graph above, domain of (f/g)(x) = [-3, 1] u (3, 4]
j) (f(3))3 - 4g(-2)
(f(3))3 - 4g(-2) = (2)3 - 4(-4)
= 8 + 16
= 24
k) For what value(s) is f(x) = 3? _______
When drawing the horizontal line at y = 3, it intersects the curve f(x) at -2, 0 and 2.
So, the respective x values are -2, 0 and 2.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling