HOW TO DETERMINE IN WHICH QUADRANT AN ANGLE LIES

Angles in standard position are always shown on the Cartesian plane. The x-axis and the y-axis divide the plane into four quadrants

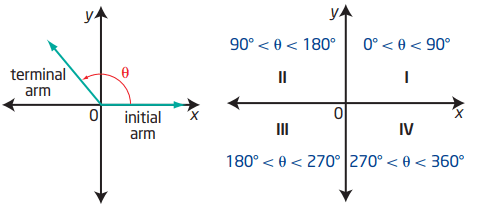
On a Cartesian plane, you can generate an angle by rotating a ray about the origin.

The starting position of the ray, along the positive x-axis, is the initial arm of the angle. The final position, after a rotation about the origin, is the terminal arm of the angle.

An angle is said to be an angle in standard position if its vertex is at the origin of a coordinate grid and its initial arm coincides with the positive x-axis.

Problem 1 :

In which quadrant does the terminal arm of each angle lie?

a) 75˚      b) 105˚     c) 225˚     d) 320˚

Solution :

i) 75˚

Since 75˚ is between 0˚ and 90˚, it is in quadrant I.

ii) 105˚

Since 105˚ is between 90˚ and 180˚, it is in quadrant II.

iii) 225˚

Since 225˚ is between 180˚ and 270˚, it is in quadrant III.

iv) 320˚

Since 320˚ is between 270˚ and 360˚, it is in quadrant IV.

Problem 2 :

Sketch each angle in standard position. State the quadrant in which the terminal arm lies.

a) 36°     b) 210°      c) 315°

Solution :

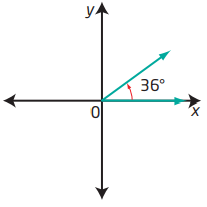
a) θ = 36° Since 0° < θ < 90°, the terminal arm of θ lies in quadrant I

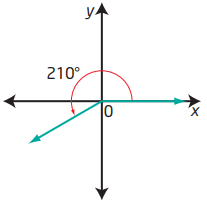
b)  θ = 210° Since 180° < θ < 270°, the terminal arm of θ lies in quadrant III.

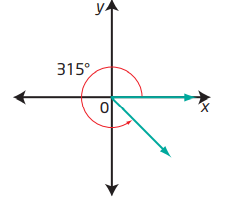
c) θ = 315° Since 270° < θ < 360°, the terminal arm of θ lies in quadrant IV.

Problem 3 :

Without measuring, match each angle with a diagram of the angle in standard position.

a) 150°     b) 180°     c) 45°     d) 320°     e) 215°     f) 270°

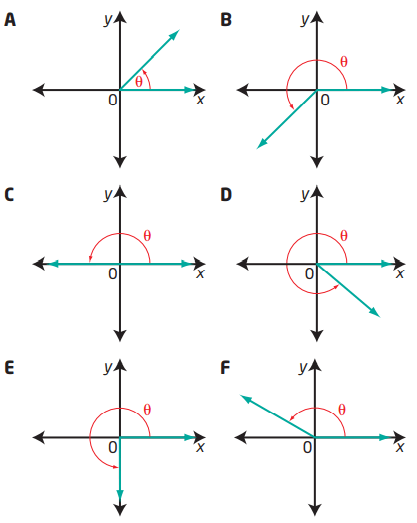
Solution :

a) 150°

Let θ = 150°

Considering θ, it lies 90° < θ < 180°. The terminal side should be in II ^nd quadrant.

So, option F.

b) 180°

Let θ = 180°

Considering θ. The terminal side should be at the end of II ^nd quadrant.

So, option C.

c) 45°

Let θ = 45°

Considering θ, it lies 90° < θ < 180°. The terminal side should be in I^st quadrant.

So, option A.

d) 320°

Let θ = 320°

Considering θ, it lies 270° < θ < 360°. The terminal side should be in IV^th quadrant.

So, option D.

e) 215°

Let θ = 215°

Considering θ, it lies 180° < θ < 215°. The terminal side should be in III^rd quadrant.

So, option B.

f) 270°

Let θ = 270°

Considering θ. The terminal side should be at the end of III^rd quadrant.

So, option E.