HOW TO DETERMINE IF THE ORDERED PAIR IS A FUNCTION

If each input associates with one output, then it is a function.

In the given set of ordered pairs, by drawing the arrow diagram, we can easily find whether the set of ordered pair is a relation or not.

Consider the following examples,

1)  {(a, 1) (b, 1) (b, 3)}

2)  {1, a) (2, b) (3, a)}

By drawing arrow diagram, we get

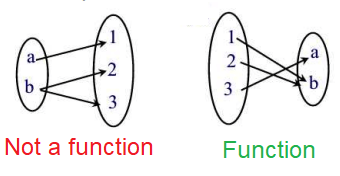
Tell whether the relation is a function. Explain.

Problem 1 :

 (3, -2), (0, 1), (1, 0), (-2, -1), (2, -1)

Solution :

Given, (3, -2), (0, 1), (1, 0), (-2, -1), (2, -1)

Let X be the set of inputs and Y be the set of outputs.

Inputs (X) = {3, 0, 1, -2, 2}

Outputs (Y) = {-2, 1, 0, -1, -1}

Create a mapping of the following relation,

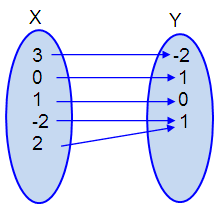
Form the arrow diagram, we understand that each x – value is being paired with only one y – value. So, it is a function.

Problem 2 :

(2, -5), (-2, 5), (-1, 4), (-2, 0), (3, -4)

Solution :

Given, (2, -5), (-2, 5), (-1, 4), (-2, 0), (3, -4)

Let X be the set of inputs and Y be the set of outputs.

Inputs (X) = {2, -2, -1, -2, 3}

Outputs (Y) = {-5, 5, 4, 0, -4}

Create a mapping of the following relation,

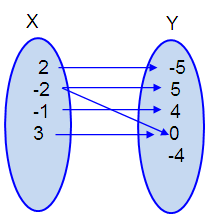
By observing the arrow diagram, one of the input has more than one output. So, it is not a function.

Problem 3 :

(0, 1), (1, 0), (2, 3), (3, 2), (4, 4)

Solution :

Given, (0, 1), (1, 0), (2, 3), (3, 2), (4, 4)

Let X be the set of inputs and Y be the set of outputs.

Inputs (X) = {0, 1, 2, 3, 4}

Outputs (Y) = {1, 0, 3, 2, 4}

Create a mapping of the following relation,

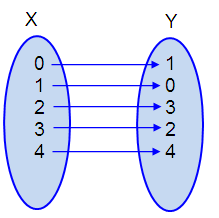
From the arrow diagram, we understand that each x – value is being paired with only one y – value. So, it is function.

Problem 4 :

(-1, -1), (2, 5), (4, 8), (-5, -9), (-1, -5)

Solution :

Given, (-1, -1), (2, 5), (4, 8), (-5, -9), (-1, -5)

Let X be the set of inputs and Y be the set of outputs.

Inputs (X) = {-1, 2, 4, -5, -1}

Outputs (Y) = {-1, 5, 8, -9, -5}

Create a mapping of the following relation,

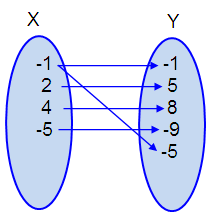
By observing the arrow diagram, one of the input has more than one output. So, it is not a function.

Problem 5 :

The relation given by the ordered pairs (-6, 3), (-2, 4), (1, 5), and (4, 0) is a function. Which ordered pair can be included with this relation to form a new relation that is also a function?

A. (1, -5)       B. (6, 3)      C. (-2, 19)      D. (4, 4)

Solution :

In options A, B and D, the first elements are 1, 6 and 4. Since it is already having outputs, by taking one of the options we will not get the function.

Option C :

By connecting the ordered pair (6, 3) with the question, we can make the relation as function.

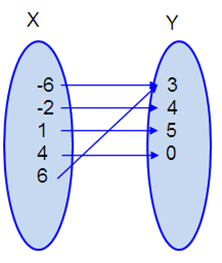
Each input value is paired with only one output value.

So, it is a function.