HOW TO CHECK WHAT TYPE OF QUADRILATERAL FROM THE GIVEN POINTS

Problem 1 :

The vertices of a quadrilateral are K(-1, 0), L(1, -2), M(4, 1) and N(2, 3). Verify that 

a) KLMN is a rectangle.

b) The lengths of the diagonals of KLMN are equal.

Solution :

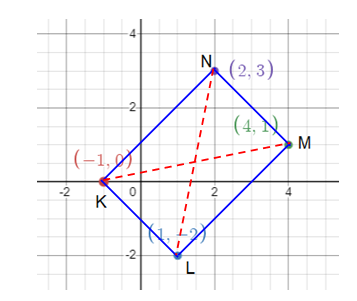
a) Given, K(-1, 0), L(1, -2), M(4, 1) and N(2, 3)

K(-1, 0) and  L(1, -2)

x₁ = -1, y₁ = 0, x₂ = 1, y₂ = -2

KL = √[(1 + 1)² + (-2 - 0)²]

= √[(2)² + (-2)²]

 = √[4 + 4]

KL =  √8

L(1, -2) and M(4, 1)

x₁ = 1, y₁ = -2, x₂ = 4, y₂ = 1

LM = √[(4 - 1)² + (1 + 2)²]

= √[(3)² + (3)²]

 = √[9 + 9]

LM =  √18

M(4, 1) and N(2, 3)

x₁ = 4, y₁ = 1, x₂ = 2, y₂ = 3

MN = √[(2 - 4)² + (3 - 1)²]

= √[(-2)² + (2)²]

 = √[4 + 4]

MN =  √8

N(2, 3) and  K(-1, 0)

x₁ = 2, y₁ = 3, x₂ = -1, y₂ = 0

NK = √[(-1 - 2)² + (0 - 3)²]

= √[(-3)² + (-3)²]

 = √[9 + 9]

NK =  √18

KL = MN and LM = NK. Opposite sides are equal.

Length of diagonal KM :

K(-1, 0) and M(4, 1)

KM = √[(4 + 1)² + (1 - 0)²]

= √[(5)² + (1)²]

 = √[25 + 1]

KM =  √26

Using Pythagorean theorem :

KM² = KL² + LM²

√26² = √8² + √18²

26 = 8 + 18

26 = 26

Length of diagonal NL :  

N(2, 3) and L(1, -2)

NL = √[(1 - 2)² + (-2 - 3)²]

= √[(-1)² + (-5)²]

 = √[1 + 25]

NL =  √26

KM = NL

b) From the above calculation, the diagonals are equal.

Diagonals are also equal.

Problem 2 :

The vertices of a quadrilateral are A(0, 0), B(2, 3), C(5, 1) and D(3, -2).

a)  Check the type of quadrilateral

b) Verify that the diagonals of ABCD are perpendicular to each other. 

Solution :

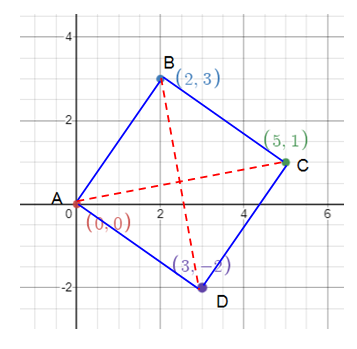
a)  Given, A(0, 0), B(2, 3), C(5, 1) and D(3, -2)

Length of AB :

A(0, 0) and B(2, 3)

AB = √[(2 - 0)² + (3 - 0)²]

= √[(2)² + (3)²]

 = √[4 + 9]

AB =  √13

Length of BC :

B(2, 3)and C(5, 1)

x₁ = 2, y₁ = 3, x₂ = 5, y₂ = 1

BC = √[(5 - 2)² + (1 - 3)²]

= √[(3)² + (-2)²]

 = √[9 + 4]

BC =  √13

Length of CD :

C(5, 1) and D(3, -2)

x₁ = 5, y₁ = 1, x₂ = 3, y₂ = -2

CD = √[(3 - 1)² + (-2 - 1)²]

= √[(2)² + (-3)²]

 = √[4 + 9]

CD =  √13

Length of DA :

D(3, -2) and A(0, 0)

x₁ = 3, y₁ = -2, x₂ = 0, y₂ = 0

DA = √[(0 - 3)² + (0 + 2)²]

= √[(-3)² + (2)²]

 = √(9 + 4)

DA =  √13

AB = BC = CD = DA all sides are equal. It may be a square or rhombus.

A(0, 0) and C(5, 1)

x₁ = 0, y₁ = 0, x₂ = 5, y₂ = 1

B(2, 3) and D(3, -2)

x₁ = 2, y₁ = 3, x₂ = 3, y₂ = -2

Slope of AC x Slope of BD = (-1/5) x 5 

= -1

Since the diagonals are perpendicular to each other, it must a rhombus.

Problem 3 :

Verify that the quadrilateral with vertices O(0, 0), P(3, 5), Q(13, 7) and R(5, 1) is a trapezoid.

Solution :

In trapezoid, there will be two parallel sides and two non parallel sides.

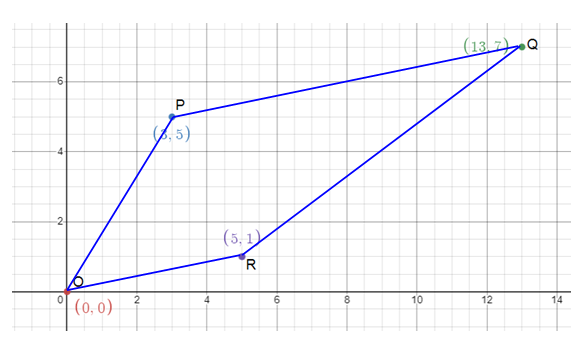
Given, O(0, 0), P(3, 5), Q(13, 7) and R(5, 1)

Slope of OP :

O(0, 0) and P(3, 5)

x₁ = 0, y₁ = 0, x₂ = 3, y₂ = 5

Slope of PQ :

P(3, 5) and Q(13, 7)

x₁ = 3, y₁ = 5, x₂ = 13, y₂ = 7

Slope of QR :

Q(13, 7) and R(5, 1)

x₁ = 13, y₁ = 7, x₂ = 5, y₂ = 1

Slope of RO :

R(5, 1) and O(0, 0)

x₁ = 5, y₁ = 1, x₂ = 0, y₂ = 0

Here the slope of the line PQ and RO are equal.

PQ = RO = 1/5

Since the pair of sides are having same slope, the given coordinate will create parallelogram.

Problem 4 :

Verify that the quadrilateral with vertices P(-2, 2), Q(-2, -3), R(-5, -5) and S(-5, 0) is a parallelogram.

Solution :

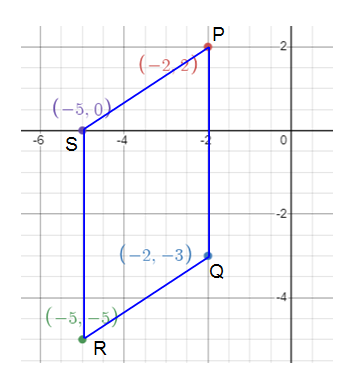
P(-2, 2) and Q(-2, -3)

x₁ = -2, y₁ = 2, x₂ = -2, y₂ = -3

Q(-2, -3) and  R(-5, -5)

x₁ = -2, y₁ = -3, x₂ = -5, y2 = -5

R(-5, -5) and S(-5, 0)

x₁ = -5, y₁ = -5, x₂ = -5, y₂ = 0

S(-5, 0) and P(-2, 2)

x₁ = -5, y₁ = 0, x₂ = -2, y₂ = 2

The opposite sides PQ, RS and QR, SP have the same slope and are thus parallel to each other.

Midpoint of the diagonals :

Midpoint of diagonal PR :

P(-2, 2) and R(-5, -5)

Midpoint of S(-5, 0) and Q(-2, -3) :

Since the midpoints of the diagonal are equal and opposite sides are equal, it must be a parallelogram.

Problem 10 :

A quadrilateral has vertices K(-1, 4), L(2, 2), M(0, -1) and N(-3, 1). Verify that :

a) The quadrilateral is a square.

b) Each diagonal of the quadrilateral is the perpendicular bisector of the other diagonal.

c) The diagonals are equal in length.Q

Solution :

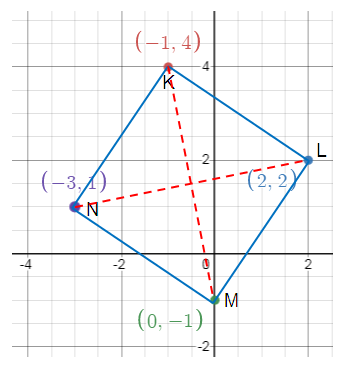
a)  Given, K(-1, 4), L(2, 2), M(0, -1) and N(-3, 1)

Length of  KL :

K(-1, 4) and L(2, 2)

x₁ = -5, y₁ = 0, x₂ = -2, y₂ = 2

KL = √[(-2 + 5)² + (2 - 0)²]

= √[(3)² + (2)²]

 = √[9 + 4]

KL = √13

Length of  LM : 

L(2, 2) and M(0, -1)

x₁ = 2, y₁ = 2, x₂ = 0 , y₂ = -1

LM = √[(0 - 2)² + (-1 - 2)²]

= √[(-2)² + (-3)²]

 = √[4 + 9]

LM = √13

Length of  MN : 

M(0, -1) and N(-3, 1)

x₁ = 0, y₁ = -1, x₂ = -3 , y₂ = 1

MN = √[(-3 - 0)² + (1 + 1)²]

= √[(-3)² + (2)²]

 = √[9 + 4]

MN = √13

Length of  NK :

N(-3, 1) and K(-1, 4) 

x₁ = -3, y₁ = 1, x₂ = -1, y₂ = 4

NK = √[(-1 + 3)² + (4 - 1)²]

= √[(2)² + (3)²]

 = √[4 + 9]

NK = √13

KL = LM = MN = NK

c) Length of  KM :

K(-1, 4) and M(0, -1)

x₁ = -1, y₁ = 4, x₂ = 0, y₂ = -1

KM = √[(0 + 1)² + (-1 - 4)²]

= √[(1)² + (-5)²]

 = √[1 + 25]

KM = √26

Length of  NL :

N(-3, 1) and L(2, 2)

x₁ = -3, y₁ = 1, x₂ = 2, y₂ = 2

NL = √[(2 + 3)² + (2 - 1)²]

= √[(5)² + (1)²]

 = √[25 + 1]

NL = √26

KM = NL

So, diagonals are equal.