HOW TO ADD AND SUBTRACT RADICAL EXPRESSIONS

To add and subtract radical expressions, we should know about like radicals and unlike radicals.

Unlike radical :

We will not have same value inside the radical sign, or we will not have same index.

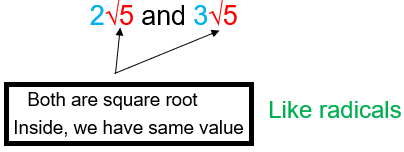
Like radical :

It means we should have the same numerical value inside the radical sign with the same index.

In front of radical sign, we may see same value or different value that doesn't matter.

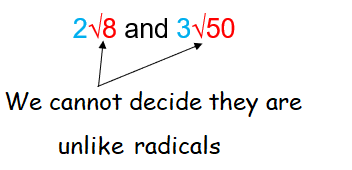
By decomposing 8 and 50, we get 

√8 = √(2 x 2 x 2) = 2√2

√50 = √(2 x 5 x 5) = 5√2

After simplification, we get the same values inside the radical sign. So, they are unlike radicals.

Problem 1 :

3√6 - 4√6

Solution :

Inside the radical signs, radicands are like terms. we can combine them.

= 3√6 - 4√6

= (3 - 4)√6

= -√6

Problem 2 :

-3√7 + 4√7

Solution :

Inside the radical signs, radicands are like terms. we can combine them.

= (-3 + 4)√7

= √7

Problem 3 :

-11√21 - 11√21

Solution :

Inside the radical signs, the radicands are like terms. we can combine them.

= (-11 - 11)√21

= -22√21

Problem 4 :

-9√15 + 10√15

Solution :

= (-9 + 10)√15

= √15

Problem 5 :

-10√7 + 12√7

Solution :

= (-10 + 12)√7

= 2√7

Problem 6 :

-3√17 - 4√17

Solution :

= (-3 - 4)√17

= -7√17

Problem 7 :

-10√11 - 11√11

Solution :

= (-10 - 11)√11

= -21√11

Problem 8 :

-2√3 + 3√27

Solution :

Here the radicands are unlike terms.

Since 3 is a prime number, we cannot decompose 3 hereafter.

So, we are decomposing 27 into prime factors.

= -2√3 + 3√(3×3×3)

= -2√3 + 3∙3√3

= -2√3 + 9√3

= (-2+9)√3

= 7√3

Problem 9 :

2√6 - 2√24

Solution :

Here the radicands are unlike terms.

We cannot decompose 6 hereafter. So, we are decomposing 24 into prime factors.

= 2√6 - 2√(2×2×2×3)

= 2√6 - 2×2√(2×3)

= 2√6 - 4√6

= (2 - 4)√6

= -2√6

Problem 10 :

2√6 + 3√54

Solution :

Here the radicands are unlike terms. 

We cannot decompose 6 hereafter. So, we are decomposing 54 into prime factors.

= 2√6 + 3√(3×3×3×2)

 = 2√6 + 3×3√(3×2)

 = 2√6 + 9√6

= (2+9)√6

= 11√6

Problem 11 :

-√12 + 3√3

Solution :

Here the radicands are unlike terms.

We cannot decompose 3 hereafter. So, we are decomposing 12 into prime factors.

= √(2×2×3) + 3√3

= -2√3 + 3√3

= (-2+3)√3

= √3

Problem 12 :

3√3 - √27

Solution :

Here the radicands are unlike terms.

We cannot decompose 3 hereafter. So, we are decomposing 27 into prime factors.

= 3√3 - √(3×3×3)

= 3√3 - 3√3

= 0

Problem 13 :

3√8 + 3√2

Solution :

Here the radicands are unlike terms.

We cannot decompose 2 hereafter. So, we are decomposing 8 into prime factors.

= 3√(2×2×2) + 3√2

= 3×2√2 + 3√2

= 6√2 + 3√2

= (6 + 3)√2

= 9√2

Problem 14 :

-3√6 + 3√6

Solution :

= (-3 + 3)√6

= 0