HORIZONTAL AND VERTICAL TRANSLATION OF ABSOLUTE VALUE FUNCTIONS

A translation is a  transformation  that shifts a graph  horizontally or  vertically, but  doesn’t change  the overall shape  or orientation.

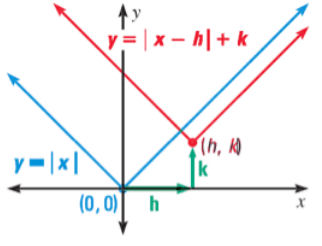
• If h > 0, then move the graph horizontally towards the right.
• If h < 0, then move the graph horizontally towards the left.
• If k > 0, then move the graph vertically up.
• If k < 0, then move the graph vertically down.

Describe the translation from the graph of f(x) = ∣x - h∣ + k to the graph of the given function. Here (h, k) be (0, 0). Then graph the given function

Problem 1 :

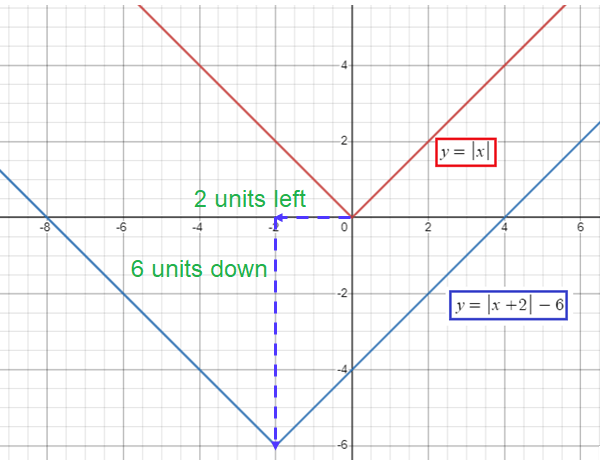
f(x) = |x + 2| - 6

Solution :

Comparing the given function with y = |x - h| + k

f(x) = |x - (-2)| + (-6)

h = -2 < 0 and k = -6 < 0

Changes needed :

Move the graph of parent function 2 units to the left and 6 units down.

Problem 2 :

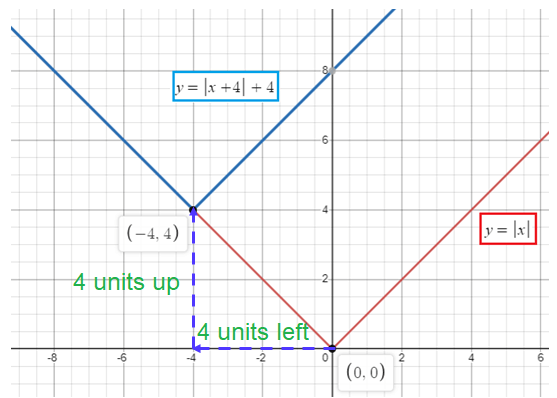
f(x) = |x + 4| + 4

Solution :

Comparing the given function with y = |x - h| + k

f(x) = |x - (-4)| + 4

h = -4 < 0 and k = 4 > 0

Changes needed :

Move the graph of parent function 4 units to the left and 4 units up.

Problem 3 :

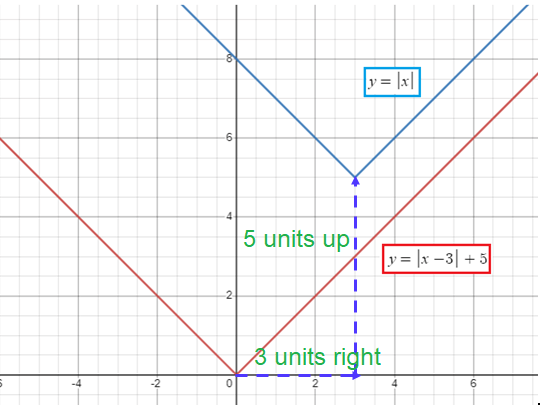
f(x) = |x - 3| + 5

Solution :

Comparing the given function with y = |x - h| + k

f(x) = |x - 3| + 5

h = 3 > 0 and k = 5 > 0

Changes needed :

Move the graph of parent function 3 units to the right and 5 units up.

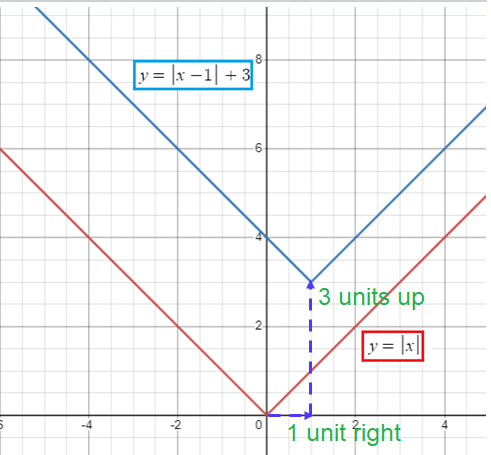
Problem 4 :

f(x) = |x - 1| + 3

Solution :

Comparing the given function with y = |x - h| + k

f(x) = |x - 1| + 3

h = 1 > 0 and k = 3 > 0

Changes needed :

Move the graph of parent function 1 unit to the right and 3 units up.

Problem 5 :

Describe and correct the error in graphing the function.

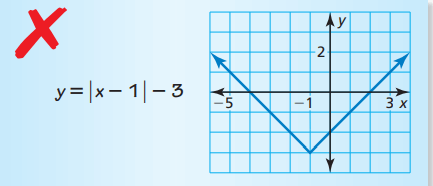
Solution :

Comparing the given equation y = |x - 1| - 3 with the parent function y = |x - h| + k

h = 1 and k = 3

• h = 1 > 0, move the graph 1 unit towards right side from the origin.
• k = -3 < 0, move the graph 3 units towards left.

In the given graph, it is moved 3 units down. Instead of moving to the right, it is moved to the left. So, this is the error.

Problem 6 :

Compare the graphs. Find the value of h and k 

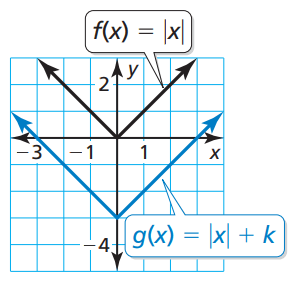
Solution :

The parent function y = |x| is moved down 2 units and there is no horizontal translation.

horizontal movement = 0 units

Vertical movement = -2 (since moving down)

Problem 7 :

Compare the graphs. Find the value of h and k 

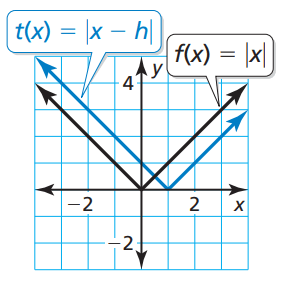
Solution :

The parent function y = |x| is moved to the right 1 unit and there is no vertical translation.

horizontal movement = 1 unit

Vertical movement = 0

Write an equation that represents the given transformation(s) of the graph of g(x) = ∣x ∣ .

Problem 8 :

(i)  Vertical translation 7 units down.

(ii)  Horizontal translation 10 units left

Solution :

(i)  Vertical translation (k) = -7 (down)

y = |x| - 7

(ii)  Horizontal translation (k) = 10 (left)

y = |x - 10|