HORIZONTAL AND VERICAL DILATION WITH EQUATION OF CIRCLE

Dilations are enlargements or reductions.

The transformation equation for a dilation with center (0, 0) and factor k are x' = kx and y' = ky

• If k > 1, the image figure is an enlargement of the object
• If 0 < k < 1, the image figure is an reduction of the object.

Vertical dilation with fixed y-axis :

Suppose P(x, y) moves P'(x', y') such that P' lies on the line through N(0, y) and P, and

we call this a horizontal dilation with the factor k.

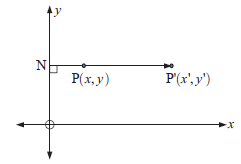
For a horizontal dilation with factor k, the transformation equation are 

x' = kx and y' = y

Vertical dilation with fixed x-axis :

Suppose P(x, y) moves P'(x', y') such that P' lies on the line through N(x, 0) and P, and

we call this a vertical dilation with the factor k.

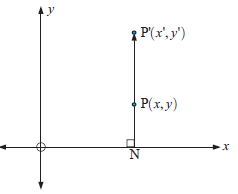
For a vertical dilation with factor k, the transformation equation are 

x' = x and y' = ky

Problem 1 :

Find the image of a circle with center O and radius 3 units, under horizontal dilation with factor 2.

Solution :

Equation of circle with center will be in the form 

x² + y² = r²

Here radius (r) = 3

x² + y² = 3²

Horizontal dilation will affect the value x only.

x' = kx and y' = y

here the factor = 2 = k

x' = 2x and y' = y

x = x'/2 and y = y'

(x/2)² + y² = 3²

(x²/4) + y² = 3²

x² + 4y² = 4(3²)

x² + 4y² = 36

Problem 2 :

Find the image of a circle with center O and radius 2 units, under a dilation with center O and factor 3/2.

Solution :

Equation of circle with center will be in the form 

x² + y² = r²

Here radius (r) = 2

x² + y² = 2²

dilation will affect the values x and y.

x' = kx and y' = ky

here the factor = 2 = k

x' = 2x and y' = 2y

x = x'/2 and y = y'/2

(x'/2)² + (y'/2)²  = 2²

(x'²/4) + (y'²/4) = 4

Changing x' and y' as x and y respectively.

x² + y² = 4(4)

x² + y² = 16

Problem 3 :

Find the image of a circle with center O and radius 2 units, under vertical dilation with factor 3/2

Solution :

Equation of circle with center will be in the form 

x² + y² = r²

Here radius (r) = 2

x² + y² = 2²

Vertical dilation will affect the value y only.

x' = x and y' = ky

here the factor = 3/2 = k

x' = x and y' = (3/2)y

x = x' and y = 2y'/3

x'² + (2y'/3)² = 4

9x'² + 4y'² = 36

Changing x' and y' as x and y respectively.

9x² + 4y² = 36

Problem 4 :

Find the image of a circle with center O and radius 2 units, under horizontal dilation with factor 3/2

Solution :

Equation of circle with center will be in the form 

x² + y² = r²

Here radius (r) = 2

x² + y² = 2²

horizontal dilation will affect the value x only.

x' = kx and y' = y

here the factor = 3/2 = k

x' = (3/2)x and y' = y

x = 2x'/3 and y = y'

(2x'/3)² + y'² = 4

4x'² + 9y'² = 36

Changing x' and y' as x and y respectively.

4x² + 9y² = 36