HONOR GEOMETRY PRACTICE PROBLEMS ON POLYGONS WITH SOLUTION 

Problem 1 :

The measure of one exterior angle of a regular polygon is given. Find the number of sides for each.

a) 72°     b) 40°

Solution:

a)

Sum of the exterior angles of regular polygon = 360°

Each exterior angle = 72°

Number of sides of regular polygon = 360°/72°

= 5

b)

Sum of the exterior angles of regular polygon = 360°

Each exterior angle = 40°

Number of sides of regular polygon = 360°/40°

= 9

Problem 2 :

Find the measure of an interior and an exterior angle of a regular 46-gon.

Solution: 

Interior angle :

Exterior angle :

Problem 3 :

The measure of one interior angle of a regular polygon is 144°. How many sides does it have?

Solution:

Problem 4 :

Five angles of a hexagon have measures 100°, 110°, 120°, 130°, and 140°. What is the measure of the sixth angle?

Solution:

Hexagon will have 6 sides. Sum of interior angles of hexagon

= (6 - 2) 180

= 4(180)

Sum of a hexagon = 720°

sixth angle = 720° - (100 + 110 + 120 + 130 + 140)

= 720° - 600°

sixth angle = 120°

Problem 5 :

Find the value of x.

a)

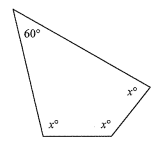
Solution:

Sum of quadrilateral = 360°

3x + 60 = 360°

3x = 360 - 60

3x = 300

x = 100°

b)

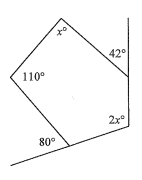
Solution:

The sum of the interior angles :

 (5 - 2) 180 = 540°

x + 110 + 100 + 2x + 138 = 540°

3x + 348 = 540

3x = 540 - 348

3x = 192

x = 64°

Problem 6 :

The sum of the interior angles of a polygon is 1620°. How many sides does it have?

Solution:

Sum of the interior angles of a polygon = (n - 2) 180°

1620 = (n - 2) 180°

n - 2 = 1620/180

n - 2 = 9

n = 11

Problem 7 :

The measure of the interior angle of a regular polygon is 179°. How many sides does it have?

Solution:

Problem 8 :

Find the value of x in the figure given.

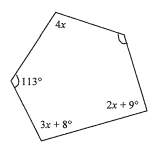
Solution:

The sum of the interior angles of a pentagon 

(5 - 2) 180 = 540°

4x + 113° + 113° + 3x + 8° + 2x + 9° = 540°

9x + 226° + 17° = 540°

9x = 540 - 243

9x = 297

x = 33°

Problem 9 :

Find the SUM of the interior angles of each polygon.

a. octagon _____

b. pentagon _____

c. hexagon _____

d. heptagon _____

Solution:

a. octagon:

Number of sides = 8

Sum of interior angle = (n - 2) × 180°

= (8 - 2) × 180°

= 6  × 180

= 1080

b. pentagon

Number of sides = 5

Sum of interior angle = (n - 2) × 180°

= (5 - 2) × 180°

= 3  × 180

= 540

c. hexagon

Number of sides = 6

Sum of interior angle = (n - 2) × 180°

= (6 - 2) × 180°

= 4  × 180

= 720

d. heptagon

Number of sides = 7

Sum of interior angle = (n - 2) × 180°

= (7 - 2) × 180°

= 5  × 180

= 900

Problem 10 :

Find the SUM of the exterior angles of each polygon.

a. octagon _____

b. pentagon _____

Solution:

a. octagon

Number of sides = 8

Sum of exterior angle = 360°

= 360/8

= 45

b. pentagon

Number of sides = 5

Sum of exterior angle = 360°

= 360/5

= 72

Problem 11 :

What is the measure of EACH interior angle of a regular:

a. octagon _____

b. pentagon _____

c. hexagon _____

d. decagon _____

Solution:

a. octagon

Number of sides = 8

(8 - 2) × 180° = 1080

Here n = 8

Each interior angle = 1080/8

= 135°

b. pentagon

Number of sides = 5

(5 - 2) × 180° = 540

Here n = 5

Each interior angle = 540/5

= 108°

c. hexagon

Number of sides = 6

(6 - 2) × 180° = 720

Here n = 6

Each interior angle = 720/6

= 120°

d. decagon

Number of sides = 10

(10 - 2) × 180° = 1440

Here n = 10

Each interior angle = 1440/10

= 144°

Problem 12 :

What is the measure of EACH exterior angle of a regular:

a. octagon _____

b. pentagon _____

c. hexagon _____ 

d. decagon _____

Solution:

a. octagon

Number of sides = 8

Measure of each exterior angle = 360°/n

= 360/8

= 45

b. pentagon

Number of sides = 5

Measure of each exterior angle = 360°/n

= 360/5

= 72

c. hexagon

Number of sides = 6

Measure of each exterior angle = 360°/n

= 360/6

= 60

d. decagon

Number of sides = 10

Measure of each exterior angle = 360°/n

= 360/10

= 36

Problem 13 :

Matching:

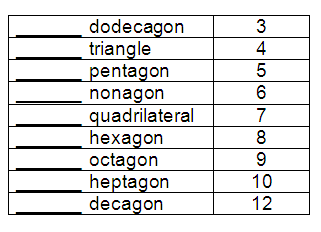
Solution:

dodecagon = 12

triangle = 3

pentagon = 5

nonagon = 9

quadrilateral = 4

hexagon = 6

octagon = 8

heptagon = 7

decagon = 10

Problem 14 :

Find the value for each variable.

a)

Solution:

n = 6

Sum of hexagon = 720°

90° + y° + y° + y° + y° + 90° = 720°

180° + 4y = 720°

4y = 720 - 180

4y = 540

y = 135°

b)

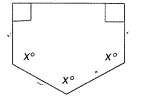
Solution:

pentagon = 5

Sum of pentagon = 540°

90° + 90° + x° + x° + x° = 540°

180° + 3x = 540°

3x = 540 - 180

3x = 360

x = 120

Problem 15 :

Find each unknown angle measure.

a)

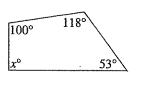
Solution:

Sum of interior angle of quadrilateral = 360°

100° + 118° + 53° + x° = 360°

271° + x = 360°

x = 360° - 271°

x = 89°

b)

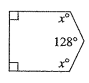
Solution:

Sum of an interior angle of a pentagon = 540°

x° + 128° + x° + 90° + 90° = 540°

2x + 308 = 540°

2x = 540 - 308

2x = 232

x = 116°

Problem 16 :

Find the measure of ∠1 in each figure.

a)

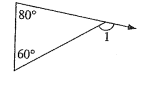
Solution:

∠1 = 60° + 80°

∠1 = 140°

b)

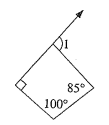
Solution:           

Sum of interior angle of rectangle is 360°.

x + 85° + 100° + 90° = 360°

x + 275° = 360°

x = 360 - 275

x = 85°

Now, sum of linear pair angle is 180°.

∠1 + x = 180°

∠1 + 85 = 180°

∠1 = 180 - 85

∠1 = 95°

Problem 17 :

Given,

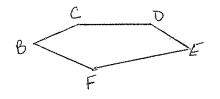
a) How many different ways can the polygon be named?

b) Name a pair of consecutive sides.

c) Name a pair of nonconsecutive vertices.

Solution :

a)  Starts with B, BCDEF and BFEDC. So, from each variable, we have two options. Then 10 ways are available.

b) For BF, FE is consecutive side. For FE, DE is consecutive side.

c) For B, D and E are non consecutive vertices.

Problem 18 :

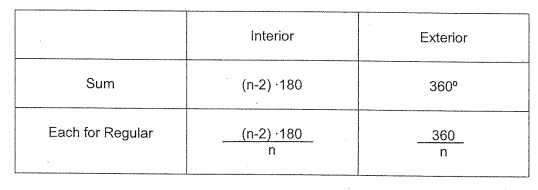
Find the sum of the interior angles of each convex polygon.

a) nonagon

b) 50-gon

Solution:

a) nonagon

Number of sides = 9

Sum of the interior angle of polygon = (n - 2) × 180°

= (9 - 2) × 180

= 6 × 180

= 1080

b) 50-gon

Number of sides = 50

Sum of the interior angle of polygon = (n - 2) × 180°

= (50 - 2) × 180

= 48 × 180

= 8640

Problem 19 :

a) Find the measure of each interior angle of a regular hexagon.

b) Find the measure of each exterior angle of a regular decagon.

Solution:

a)

Number of sides = 6

(6 - 2) × 180° = 720

Here n = 6

Each interior angle = 720/6

= 120°

b)

Number of sides = 10

Here n = 10

Each exterior angle = 360/10

= 36°

Problem 20 :

The measure of each exterior angle in a regular polygon is 24°. How many sides does the polygon have?

Solution:

Sum of exterior angle of polygon = 360°

Each exterior angle of polygon = 24

Number of sides of polygon = 360/24 = 15

So, number of sides of polygon with each angle of 24° is 15.