GRAPHS OF PROPORTIONAL RELATIONSHIPS

Problem 1 :

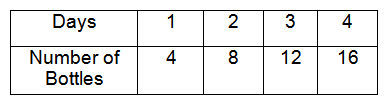
Olivia sold water bottles over four days. Create a graph to determine if the quantities of bottles and number of days are proportional. If the quantities are proportional, what is the constant of proportionality ?

Solution :

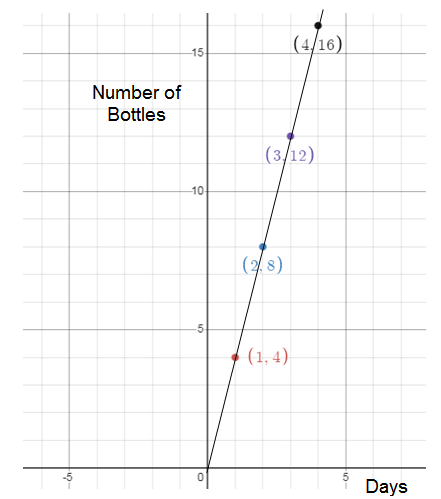
From the graph it is clear.

The table represents proportional between quantities of bottles and number of days.

Number of days = x, Number of bottles = y

y = kx

k = y/x

k = 4/1

k = 4

So, the constant of proportionality (k) is 4.

Problem 2 :

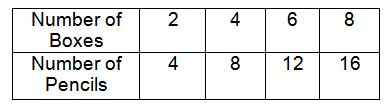
Aiden brought some pencils and boxes. Create a graph to determine if the quantities of boxes and pencils are proportional. If the quantities are proportional, what is the constant of proportionality ?

Solution :

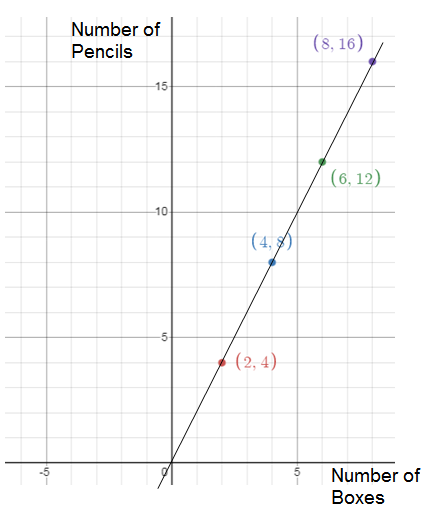
The table represents proportional between quantities of boxes and number of pencils.

Number of boxes = x, number of pencils = y

y = kx

k = y/x

k = 4/2

k = 2

So, the constant of proportionality (k) is 2.

Problem 3 :

The graph below represents the number of balls thrown over time. What is the constant of proportionality ?

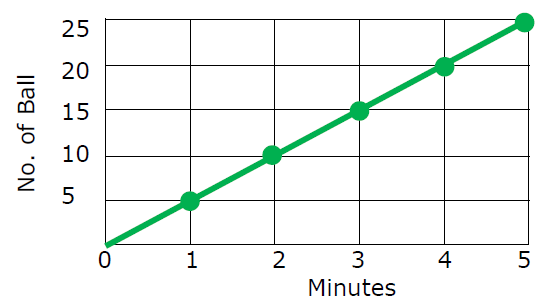
Solution :

The graph represents proportional between number of balls and minutes.

Number of Minutes = x

Number of Balls = y

y = kx

k = y/x

k = 5/1

k = 5

So, the constant of proportionality (k) is 5.

Problem 4 :

The graph below represents the number of miles Michael ran over time. What is the constant of proportionality ?

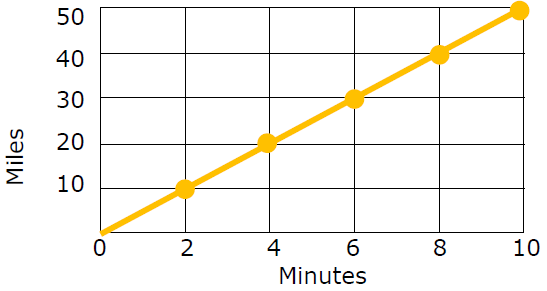
Solution :

The graph represents proportional between number of miles and minutes.

Number of Minutes = x

Number of Miles = y

y = kx

k = y/x

k = 10/2

k = 5

So, the constant of proportionality (k) is 5.

Problem 5 :

Jayden sold mobile phones over four days. Create a graph to determine if there is a proportional relationship between the data. If the quantities are proportional, what is the constant of proportionality ?

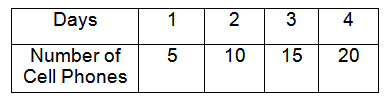
Solution :

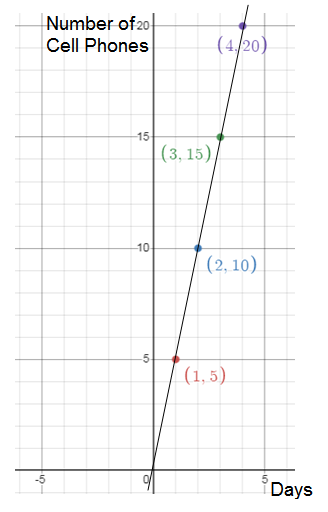
The table represents proportional between quantities of cell phones and number of days.

Number of Days = x

Number of Cell Phones = y

y = kx

k = y/x

k = 5/1

k = 5

So, the constant of proportionality (k) is 5.

Problem 6 :

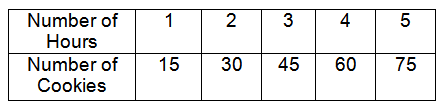
William made cookies over consecutive hours. Create a graph to determine if a proportional relationship exists between time and the number of cookies made. If the quantities are proportional, what is the constant of proportionality ?

Solution :

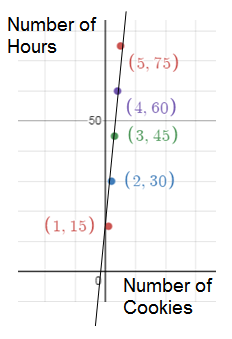
The table represents proportional between time and the number of cookies made.

Number of Cookies = x

Number of Hours = y

y = kx

k = y/x

k = 15/1

k = 15

So, the constant of proportionality (k) is 15.

Problem 7 :

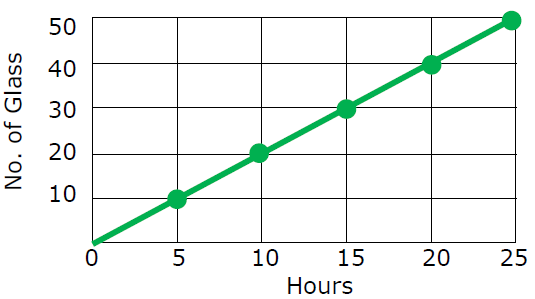
The graph below represents the number of glasses. Torn drank over time. What is the constant of proportionality ?   

Solution :

The graph represents proportional between number of glasses and hours.

Number of glasses = x

Number of hours = y

y = kx

k = y/x

k = 10/5

k = 2

So, the constant of proportionality (k) is 2.

Problem 8 :

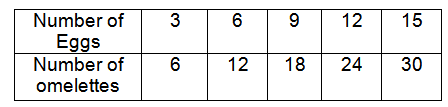
Mason made omelettes. Create a graph to determine if there is a proportional relationship between the number of eggs used and the number of omelettes made. If the quantities are proportional, what is the constant of proportionality ? 

Solution :

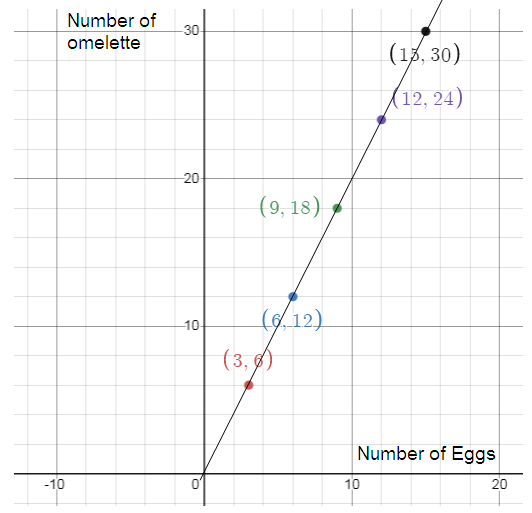
The table represents proportional between number of eggs and the number of omelets made

Number of Eggs = x

Number of omelets = y

y = kx

k = y/x

k = 6/3

k = 2

So, the constant of proportionality (k) is 2.

Problem 9 :

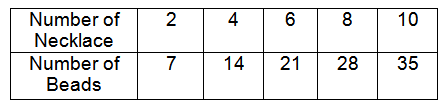
Isabella made necklaces with beads. Create a graph to determine if the quantities of beads and necklace are proportional. If the quantities are proportional, what is the constant of proportionality ?

Solution :

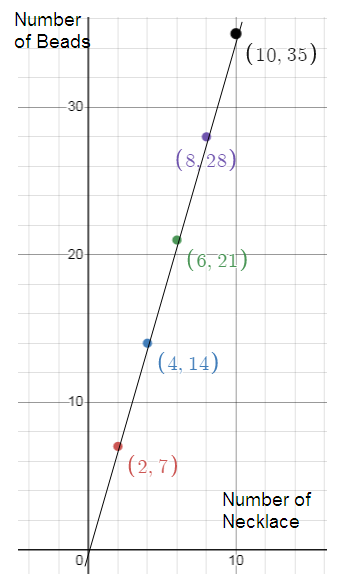
The table represents proportional between  quantities of beads and number of necklace.

Number of necklace = x

Number of beads = y

y = kx

k = y/x

k = 7/2

So, the constant of proportionality (k) is 7/2.

Problem 10 :

The graph below represents the number of vertical jumps Ava can do over time. What is the constant of proportionality ?

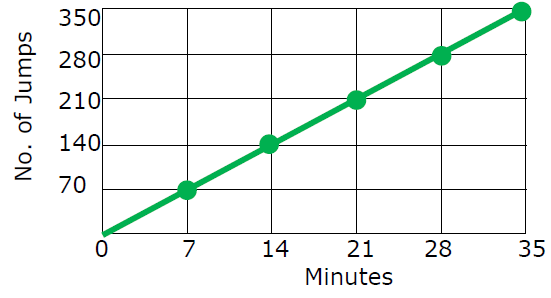
Solution :

The graph represents proportional between number of vertical jumps and minutes.

Number of minutes = x

Number of jumps = y

y = kx

k = y/x

k = 70/7

k = 10

So, the constant of proportionality (k) is 10.