GRAPHING THE INEQUALITY ON A NUMBER LINE

The relationship between two values that are not equal is defined by inequalities. Inequality means not equal. Generally, if two values are not equal, we use “not equal symbol (≠)”.

But to compare the values, whether it is less than or greater than, different inequalities are used. There are four inequalities signs are used.

<	Less than	x < 3 The values of x should be lesser than 3.
>	greater than	x > 3 The values of x should be greater than 3.
≤	Lesser than or equal	x ≤ 3 The values of x should be lesser than or equal to 3.
≥	greater than or equal	x ≥ 3 The values of x should be greater than or equal to 3.

Graphing inequality in number line

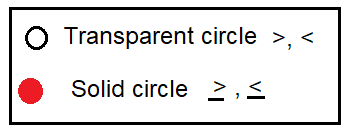
A compound inequality containing and is true only if both inequalities are true. Thus, the graph of a compound inequality containing and is the intersection of the graphs of the two inequalities.

In other words, the solution must be a solution of both inequalities.

That is, we have to shade the portion that we find in both graphs. If the particular region is not in one of the graphs, we should not shade the region.

Another type of compound inequality contains the word or. A compound inequality containing or is true if one or more of the inequalities is true. The graph of a compound inequality containing or is the of the graphs of the two inequalities.

In other words, the solution of the compound inequality is a solution of either inequality, not necessarily both. The union can be found by graphing each inequality.

Graph the inequality on a number line.

Problem 1 :

x ≤ -8

Solution :

Given, x ≤ -8

So, any real number less than or equal to -8 is a solution of the given equation.

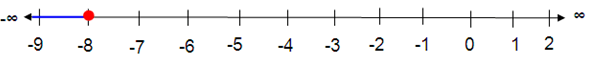
The solution set of the given inequality is (-∞, -8].

Problem 2 :

x ≥ 6

Solution :

Given, x ≥ 6

So, any real number greater than or equal to 6 is a solution of the given equation.

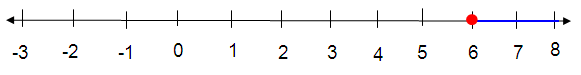
The solution set of the given inequality is [6, ∞).

Problem 3 :

-3 ≤ x ≤ 5

Solution :

-3 ≤ x ≤ 5

Any real number which lies between -3 to 5 is solution.

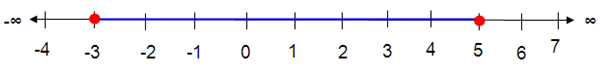
The solution set of the given inequality is [-3, 5].

Problem 4 :

x ≥ -7 and x ≤ -1

Solution :

x ≥ -7 and x ≤ -1

Any real number greater than or equal to -7 and less than or equal to -1 is a solution.

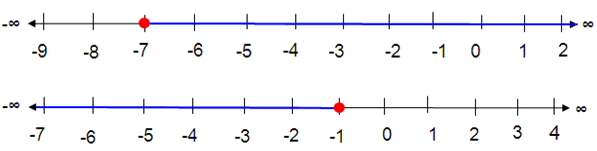
The overlapping region is the solution. The solution set of the given inequality is

[-7, -1]

Problem 5 :

x ≥ -2 or x ≤ 4

Solution :

Given, x ≥ -2 or x ≤ 4

Any real number greater than or equal to -2 and less than or equal to 4 is a solution of the given equation.

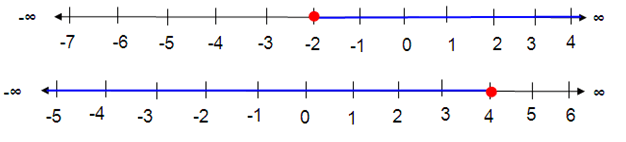
The solution set of the given inequality is (-∞, 4].

Problem 6 :

│x│≥ 0

Solution :

Given, │x│≥ 0

So, any real number greater than or equal to 0 is a solution of the given equation.

GRAPHING THE INEQUALITY ON A NUMBER LINE

Graphing inequality in number line

Recent Articles

Finding Range of Values Inequality Problems

Solving Two Step Inequality Word Problems

Exponential Function Context and Data Modeling