GRAPHING THE EXPONENTIAL FUNCTION AND FIND DOMAIN AND RANGE

The following points will be helpful to draw the graph of the exponential function.

The function which is in the form y = abx-h+ k, is known as exponential function.

  • Here y = k is the horizontal asymptote.

The sign of a will say whether it is reflection across x axis.

  • If sign of a is positive, there is no reflection.
  • If sign of a is negative, there is a reflection across x-axis.

The value of h will be horizontal translation.

  • If h > 0, then horizontal translation of right h units.
  • If h < 0, then horizontal translation of left h units.

Step 1 :

Apply some random values of x, find the values of y.

Step 2 :

Mark the coordinates in the xy-plane.

Step 3 :

Join the points, we will get the graph of exponential function.

Step 4 :

Fix the horizontal asymptote.

Sketch the graph of each exponential function by doing the following:

Sketch the asymptote, label at least three distinct coordinate points on each graph, and write the domain and range of each function.

Problem 1 :

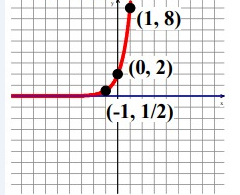
y = 2(4)x

Solution:

y = 2(4)x

Comparing the given function with y = abx-h+ k, equation of Horizontal asymptote is y = k.

Here equation of horizontal asymptote for the given function is y = 0

Coordinate points:

If x = -1,

y = 2(4)-1

= 2(1/4)

y = 1/2

If x = 1,

y = 2(4)1

y = 8

If x = 0,

y = 2(4)0

= 2(1)

y = 2

If x = 2,

y = 2(4)2

y = 32

The coordinate points are (-1, 1/2), (0, 2), (1, 8), (2, 32).

Domain:

Domain is the defined value of x. For this function, the domain is all real numbers.

Range:

The range is y > 0.

graphing-expo-fun-q1

Problem 2 :

y = -(3)x

Solution:

Comparing the given function with y = abx-h+ k, equation of Horizontal asymptote is y = k.

Here equation of horizontal asymptote for the given function is y = 0

y = -(3)x

Coordinate points:

If x = -1

y = -(3)-1

y = -1/3

If x = 1

y = -(3)1

y = -3

If x = 0

y = -(3)0

y = -1

If x = 2

y = -(3)2

y = -9

The coordinate points are (-1, -1/3), (0, -1), (1, -3), (2, -9).

Domain:

Domain is the defined value of x. For this function, the domain is all real numbers.

Range:

The range is y < 0.

graphing-expo-fun-q2.png

Problem 3 :

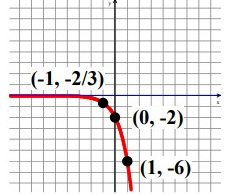
y = -2(3)x

Solution:

Comparing the given function with y = abx-h+ k, equation of Horizontal asymptote is y = k.

Here equation of horizontal asymptote for the given function is y = 0

Coordinate points:

If x = -1

y = -2(3)-1

y = -2/3

If x = 1,

y = -2(3)1

y = -6

If x = 0,

y = -2(3)0

y = -2

If x = 2,

y = -2(3)2

y = -18

The coordinate points are (-1, -2/3), (0, -2), (1, -6), (2, -18).

Domain:

Domain is the defined value of x. For this function, the domain is all real numbers.

Range:

The range is y < 0.

graphing-expo-fun-q3.png

Problem 4 :

y = (2)x+4 + 1

Solution:

Comparing the given function with y = abx-h+ k, equation of Horizontal asymptote is y = k.

Here equation of horizontal asymptote for the given function is y = 1

y = (2)x+4 + 1

Coordinate points:

If x = -2

y = (2)-2+4 + 1

= (2)2 + 1

y = 5

If x = -4

y = (2)-4+4 + 1

= (2)0 + 1

y = 2

If x = -3

y = (2)-3+4 + 1

= (2)1 + 1

y = 3

If x = -5

y = (2)-5+4 + 1

= (2)-1 + 1

y = 3/2

The coordinate points are (-2, 5), (-3, 3), (-4, 2), (-5, 3/2).

Domain:

Domain is the defined value of x. For this function, the domain is all real numbers.

Range:

The range is y > 1.

graphing-expo-fun-q4.png

Problem 5 :

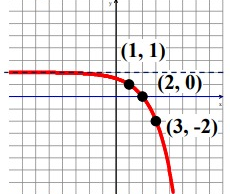
y = -2(2)x-2 + 2

Solution:

Comparing the given function with y = abx-h+ k, equation of Horizontal asymptote is y = k.

Here equation of horizontal asymptote for the given function is y = 2

Coordinate points:

If x = 1,

y = -2(2)1-2 + 2

= -2(2)-1 + 2

= -2(1/2) + 2

= -1 + 2

y = 1

If x = 3,

y = -2(2)3-2 + 2

= -2(2)1 + 2

= -2(2) + 2

= -4 + 2

y = -2

If x = 2,

y = -2(2)2-2 + 2

= -2(2)0 + 2

= -2(1) + 2

y = 0

If x = 4,

y = -2(2)4-2 + 2

= -2(2)2 + 2

= -2(4) + 2

= -8 + 2

y = -6

The coordinate points are (1, 1), (2, 0), (3, -2), (4, -6).

Domain:

Domain is the defined value of x. For this function, the domain is all real numbers.

Range:

The range is y < 2.

graphing-expo-fun-q5.png

Problem 6 :

y = 3(3)x+2 - 4

Solution:

Comparing the given function with y = abx-h+ k, equation of Horizontal asymptote is y = k.

Here equation of horizontal asymptote for the given function is y = -4

Coordinate points:

If x = -1,

y = 3(3)-1+2 - 4

= 3(3)1 - 4

= 9 - 4

y = 5

If x = -3,

y = 3(3)-3+2 - 4

= 3(3)-1 - 4

= 1 - 4

y = -3

If x = -2,

y = 3(3)-2+2 - 4

= 3(3)0 - 4

y = -1

If x = -4,

y = 3(3)-4+2 - 4

= 3(3)-2 - 4

y = -11/3

The coordinate points are (-1, 5), (-2, -1), (-3, -4), (-4, -11/3).

Domain:

Domain is the defined value of x. For this function, the domain is all real numbers.

Range:

The range is y > -3.

graphing-expo-fun-q6.png

Recent Articles

RSS

  1. Finding Range of Values Inequality Problems

    May 21, 24 08:51 PM

    Finding Range of Values Inequality Problems

    Read More

  2. Solving Two Step Inequality Word Problems

    May 21, 24 08:51 AM

    Solving Two Step Inequality Word Problems

    Read More

  3. Exponential Function Context and Data Modeling

    May 20, 24 10:45 PM

    Exponential Function Context and Data Modeling

    Read More