GRAPHING SYSTEMS OF INEQUALITIES

Sketch the graph of the system of linear inequalities. 

Example 1 :

2x + 1 > 0

3y - 6 > 0

Solution :

Given,

2x + 1 > 0 and 3y - 6 > 0

Converting the inequalities into equations.

2x + 1 = 0 and 3y - 6 = 0

By plotting the x and y values on the graph, we get

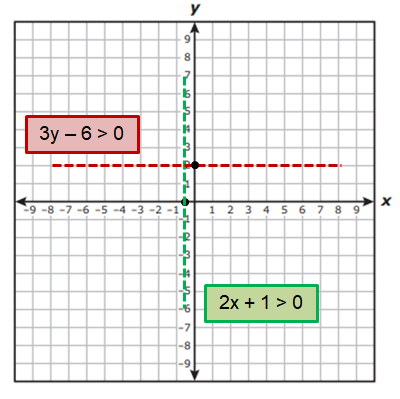
If x = 0, then 2(0) + 1 > 0 (True)

So, we can shade the region which is right to 2x + 1 > 0

If y = 3, then 3(3) - 6 > 0 (True)

So, we can shade the region which is above to 3y - 6 > 0

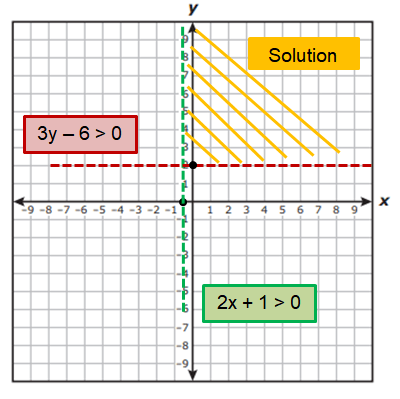
Example 2 :

2x + 3y ≥ 6

4x + 6y ≤ 24

Solution :

Given,

2x + 3y ≥ 6 and 4x + 6y ≤ 24

Converting the inequalities into equations.

2x + 3y = 6 and 4x + 6y = 24

To graph the line 2x + 3y  =  6, we find x and y intercepts.

To graph the line 4x + 6y = 24, we find x and y intercepts.

The point on the line 2x + 3y = 6 are (3, 0) and (0, 2)

The point on the line 4x + 6y = 24 are (6, 0) and (0, 4)

By plotting the points on the graph, we get

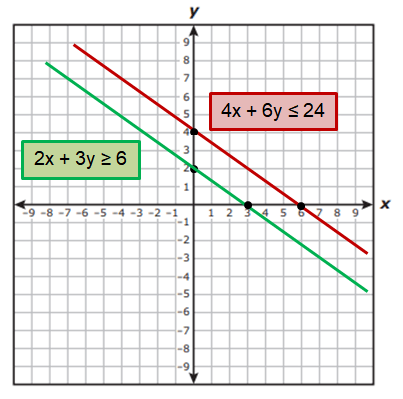
If x = 4 and y = 3, then 2(4) + 3(3) ≥ 6 (True)

So, we can shade the region which is above to 2x + 3y ≥ 6.

If x = 2 and y = 2, then 4(2) + 6(2) ≤ 24 (True)

So, we can shade the region which is below to 4x + 6y ≤ 24.

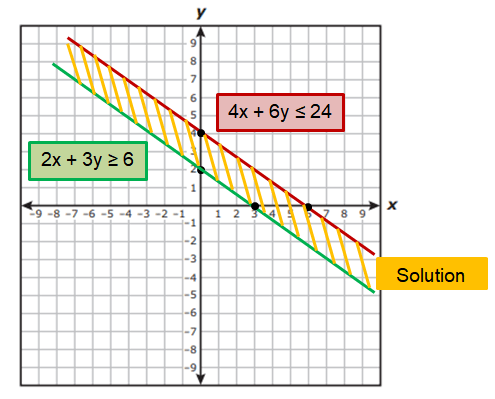
Example 3 :

2y - x ≥ -6

2y - 3x < -6

Solution :

Given,

2y - x ≥ -6 and 2y - 3x < -6

Converting the inequalities into equations.

2y - x = -6 and 2y - 3x = -6

To graph the line 2y - x = -6, we find x and y intercepts.

To graph the line 2y - 3x = -6, we find x and y intercepts.

The point on the line 2y - x = -6 are (6, 0) and (0, -3)

The point on the line 2y - 3x = -6 are (2, 0) and (0, -3)

By plotting the points on the graph, we get

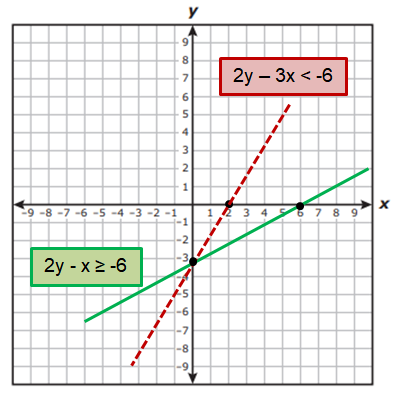
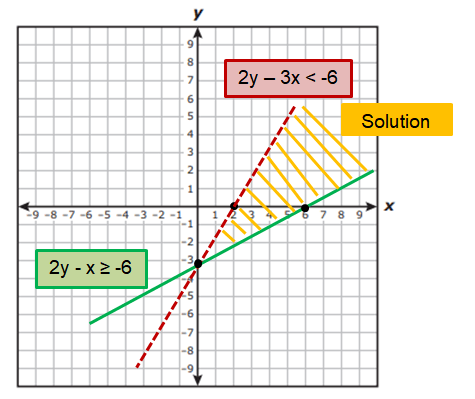
If x = 3 and y = 0, then 2(0) - 3 ≥ -6 (True)

So, we can shade the region which is above to 2y - x ≥ -6.

If x = 3 and y = -5, then 2(-5) - 3(3) < -6 (True)

So, we can shade the region which is below to 2y - 3x < -6

Example 4 :

Write a system of linear inequalities represented by the graph.

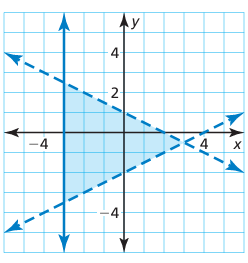
Solution :

Inequality represented by the solid line :

The solid line passes through the point (-3, 0). It's shaded region is toward the right of the line. Then x ≥ -3

Inequality represented by the falling line :

Two of the points joining the line are (0, 1) and (2, 0)

y-intercept = 2

Slope = (0 - 1) / (2 - 0)

= 1/2

y = mx + b

y = (1/2)x + 1

The shaded region is below the line, then the inequality sign suits for the situation is <.

y < (1/2)x + 1

Inequality represented by the raising line :

Two of the points joining the line are (-4, -4) and (0, -2)

y-intercept = -2

Slope = (-2 + 4) / (0 + 4)

= 2/4

= 1/2

y = mx + b

y = (1/2)x - 2

The shaded region is below the line, then the inequality sign suits for the situation is >.

y > (1/2)x + 1

So, the inequalities represented by the shaded region are

x ≥ -3

y < (1/2)x + 1

y > (1/2)x + 1

Example 5 :

You are buying movie passes and gift cards as prizes for an event. You need at least five movie passes and two gift cards. A movie pass costs $6 and a gift card costs $10. The most you can spend is $70. 

a. Write and graph a system of linear inequalities that represents the situation.

b. Identify and interpret two possible solutions.

Solution :

a)  Let x be the number of passes for movie and y be the number of gift cards.

x ≥ 5 and y ≥ 2

6x + 10y ≤ 70

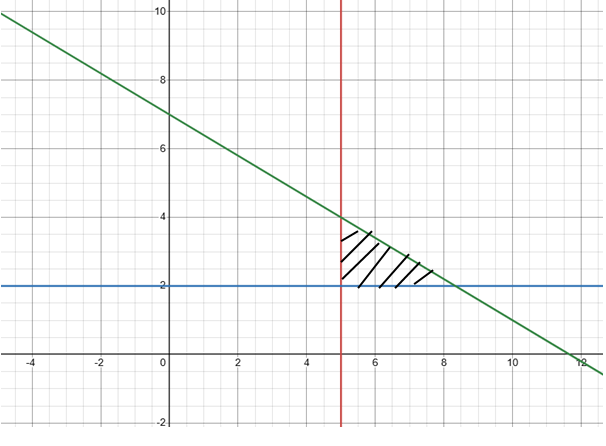
b)  Possible solutuons are (5, 2) and (6, 3)

6x + 10y ≤ 70

When number of movie tickets = 5, number of gift cards = 2

6(5) + 10(2) ≤ 70

30 + 20 ≤ 70

50 ≤ 70

When number of movie tickets = 6, number of gift cards = 3

6(6) + 10(3) ≤ 70

36 + 30 ≤ 70

66 ≤ 70