GRAPHING SQUARE ROOT FUNCTIONS

The radical function in the form y = √(x - a) + b can be graphed easily by comparing with the graph of parent function y = √x

Domain :

The domain is all possible value of x.

For √x, domain is x≥0.

Horizontal translation :

Horizontal translation is shifting the base graph left or right in the direction of the x-axis.

In √(x - a), we move the parent function a units to the right
In √(x + a), we move the parent function a units to the left.

Vertical translation :

Horizontal translation is shifting the base graph up or down in the direction of the y-axis.

In √x + b, we move the parent function b units up.
In √x - b, we move the parent function b units down.

Horizontal or vertical compressions :

Given a function f(x), a new function g(x) = a g(x) where a is a constant.

If a > 1, then the graph will be stretched
If 0 < a < 1, then the graph will be compressed.
If a < 0, then there will be reflection.

Intercepts :

To find x-intercept, we will put y = 0 and solve for x.

To find y-intercept, we will put x = 0 and solve for y.

Graph each of the function given below.

Example 1 :

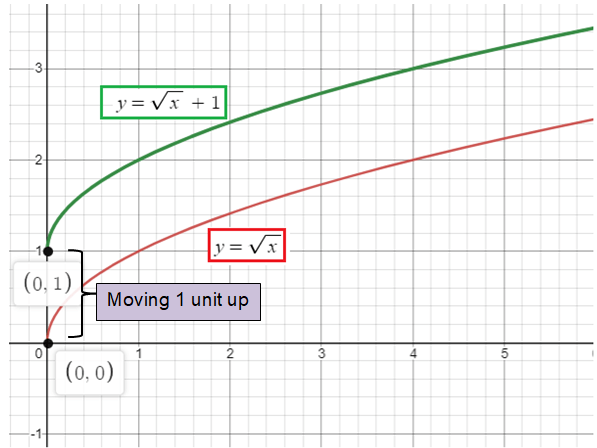
y = √x + 1

Solution :

By considering the parent function y = √x

1 is added along with the parent function, so there is vertical translation. We have to move the graph 1 unit up.

Example 2 :

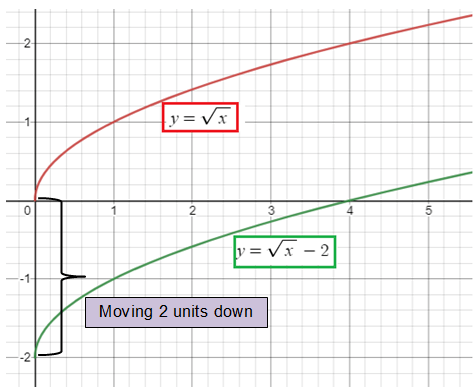
y = √x - 2

Solution :

By considering the parent function y = √x

2 is subtracted from the parent function, so there is vertical translation. We have to move the graph 2 units down.

Example 3 :

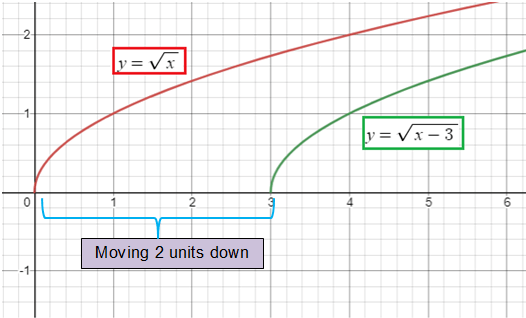
y = √(x - 3)

Solution :

By considering the parent function y = √x

3 is subtracted from x, so there will be a horizontal translation.

We have to move the graph, 3 units to the right.

Example 4 :

y = 3√(x + 1) + 4

Solution :

By considering the parent function y = √x

1 is added with x, so we have to perform horizontal translation. Move the graph 1 unit to the left.

4 is added with the parent function, so we have to perform vertical translation. Move the graph 4 units up.

3 is multiplied with the parent function, we have to stretch 3 units.

x intercept :

Put y = 0

0 = 3√(x + 1) + 4

-4/3 = √(x + 1)

There is no x-intercept.

y intercept :

Put x = 0

y = 3√(0 + 1) + 4

y = 3 + 4

y = 7

(0, 7)

GRAPHING SQUARE ROOT FUNCTIONS

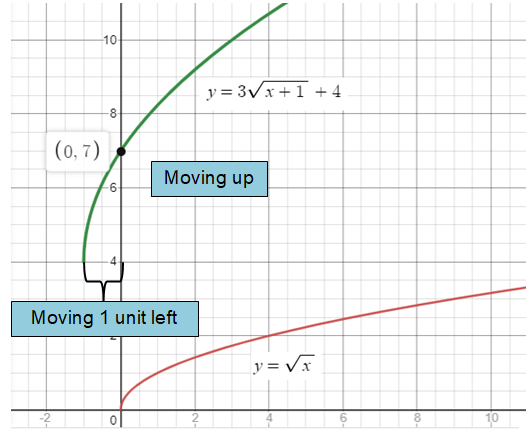
Recent Articles

Finding Range of Values Inequality Problems

Solving Two Step Inequality Word Problems

Exponential Function Context and Data Modeling