GRAPHING SQUARE ROOT FUNCTIONS EXAMPLES

The radical function in the form y = a√(x - h) + k can be graphed easily by comparing with the graph of parent function y = √x

Before start drawing the graph of square root function, it is must to discuss about domain and range of the function.

Set of all possible inputs is called domain of a particular function.

Square root function which is in the form of

y = √x

the function will be defined only for positive values.
for the value 0 also it is defined.
for negative values it is undefined.
So, domain is x ≥ 0

Set of possible outputs is called range of the function. For the function above,

range is all positive values including 0.
So, range is y ≥ 0

The situation to use the concept of transformation :

y = a √(x - h) + k

If h > 0, then move the graph right h units.
If h < 0, then move the graph left h units.
If k > 0, then move the graph up k units.
If k < 0, then move the graph down k units.
If sign of a is negative, reflection is done.

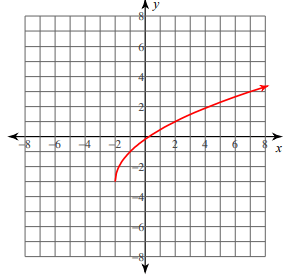
Problem 1 :

f(x) = 2√(x + 2) - 3

Solution :

Finding domain :

√(x + 2) ≥ 0

Taking square on both sides.

x + 2 ≥ 0

Subtract 2 on both sides

x ≥ -2

Finding range :

here k = -3, move the graph 3 units down and there is no reflection.

f(x) ≥ -3

So, the range is [-3, ∞)

Transformation :

Here h = -2, move the graph 2 units left.
k = -3, move the graph 3 units down.
a = 2, horizontal stretch of 2 units

Problem 2 :

f(x) = √(x - 3)

Solution :

Finding domain :

√(x - 3) ≥ 0

Taking square on both sides.

x - 3 ≥ 0

Add 3 on both sides.

x ≥ 3

So, the domain is (3, ∞)

Finding range :

here k = 0, then don't have to move the graph from origin. The curve should start from 0 and move upto ∞.

f(x) ≥ 0

So, the range is [0, ∞)

Transformation :

Here h = 3, move the graph 2 units right.
k = 0, don't have to move the graph from origin.
a = 1, no horizontal stretch or compression.

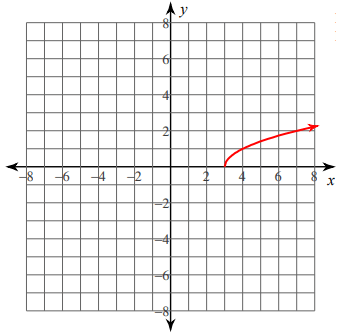
Problem 3 :

f(x) = 3√(x - 4)

Solution :

Finding domain :

√(x - 4) ≥ 0

Taking square on both sides.

x - 4 ≥ 0

Add 4 on both sides.

x ≥ 4

So, the domain is (4, ∞)

Finding range :

here k = 0, then don't have to move the graph from origin. The curve should start from 0 and move upto ∞.

f(x) ≥ 0

So, the range is [0, ∞)

Transformation :

Here h = 4, move the graph 4 units right.
k = 0, don't have to move the graph from origin.
a = 3, horizontal stretch of 3 units.

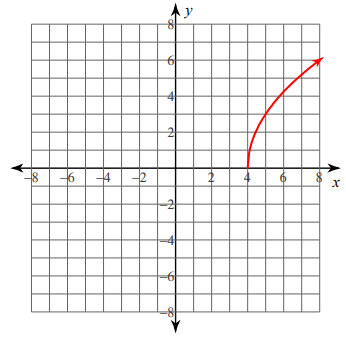
Problem 4 :

f(x) = √x - 4

Solution :

Finding domain :

√x ≥ 0

Taking square on both sides.

x ≥ 0

So, the domain is (0, ∞)

Finding range :

here k = -4, move the graph 4 units down.

f(x) ≥ -4

So, the range is [-4, ∞)

Transformation :

Here h = 0, don't have to move the graph from origin.
k = -4, move the graph down 4 units.
a = 1, no horizontal stretch or compression.

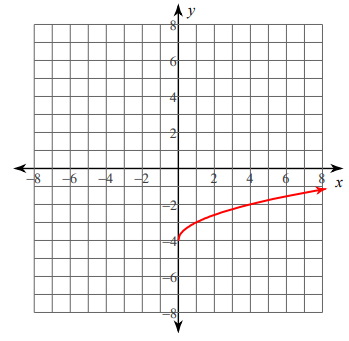
Problem 5 :

f(x) = -√(3x - 5) + 5

Solution :

Finding domain :

√(3x - 5) ≥ 0

Taking square on both sides.

3x - 5 ≥ 0

Add 5 on both sides and then divide by 3

x ≥ 5/3

So, the domain is [5/3, ∞)

Finding range :

here k = 5, move the graph 5 units up

a = -1, there is a reflection

f(x) ≥ 5

So, the range is (-∞, 5]

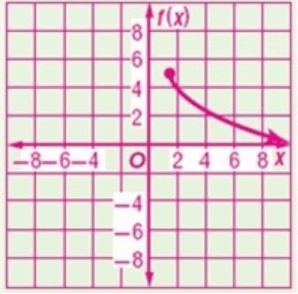
Problem 6 :

Solution :

Finding domain :

√(x + 4) ≥ 0

Taking square on both sides.

x + 4 ≥ 0

Subtract 4 on both sides.

x ≥ -4

So, the domain is [-4, ∞)

Finding range :

here k = -1, move the graph 1 units down.

a = 1/2, there is horizontal compression of 1/2 units and there is no reflection.

f(x) ≥ -1

So, the range is [-1, ∞)

GRAPHING SQUARE ROOT FUNCTIONS EXAMPLES

Recent Articles

Finding Range of Values Inequality Problems

Solving Two Step Inequality Word Problems

Exponential Function Context and Data Modeling