GRAPHING RATIONAL FUNCTION EXAMPLES

To know about continuity, holes, vertical asymptotes, horizontal asymptotes, and domain. Click on the link

Graphing rational function

Identify the points of discontinuity, holes, vertical asymptotes, x – intercepts, horizontal asymptote, and domain of each. Then sketch the graph.

Example 1 :

f(x) = (x² - 7x + 12)/(-2x² - 2x + 24)

Solution :

Discontinuity :

f(x) = (x² - 7x + 12)/(-2x² - 2x + 24)

= (x² - 7x + 12)/-2(x² + x - 12)

By factoring,

x² - 7x + 12 = (x – 3) (x – 4)

2(x² + x – 12) = (x - 3) (x + 4)

f(x) = (x – 3) (x – 4)/(x - 3) (x + 4)

x - 3 = 0 and x + 4 = 0

x = 3 and x = -4

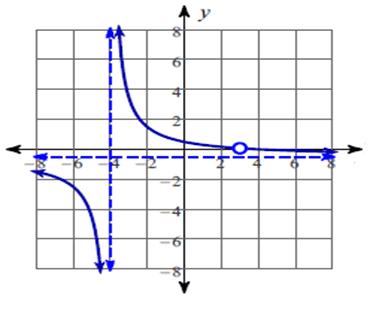
The function is discontinuous at x = 3 and x = -4.

Holes :

The common factor is (x - 3).

x – 3 = 0

x = 3

So, there is a hole at x = 3.

Vertical asymptote :

x + 4 = 0

x = -4

So, the vertical asymptote at x = -4.

X – intercepts :

f(x) = (x – 3) (x – 4)/(x - 3) (x + 4)

X – intercepts occurs when y = 0.

f(0) = (x - 4)/(x + 4)

x - 4 = 0

x = 4

So, the x – intercepts is 4.

Horizontal asymptote :

f(x) = (x² - 7x + 12)/-2(x² + x - 12)

degree of numerator = degree of denominator

y = leading coefficient of N(x)/leading coefficient of D(x).

= 1/-2

So, equation of the horizontal asymptote is y = -1/2.

Domain :

When x - 3 = 0 and x + 4 = 0

x = 3 and x = -4

So, all real values except 3 and -4.

Example  2 :

f(x) = (3x² - 3x - 18)/(x² - 4)

Solution :

Discontinuity :

f(x) = (3x² - 3x - 18)/(x² - 4)

By factoring,

3x² - 3x – 18 = 3(x² – x – 6)

3(x² – x – 6) = 0

x² – x – 6 = (x + 2) (x – 3)

x² – 4 = (x + 2) (x – 2)

f(x) = (x + 2) (x – 3)/(x + 2) (x – 2)

  (x + 2) (x – 2) = 0

x + 2 = 0 and x – 2 = 0

x = -2, x = 2

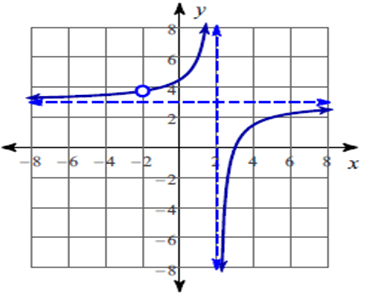
The function is discontinuous at  x = 2 and x = -2.

Holes :

The common factor is (x + 2).

x + 2 = 0

x = -2

So, there is a hole at x = -2.

Vertical asymptote :

x – 2 = 0

x = 2

So, the vertical asymptotes at x = 2.

X – intercepts :

f(x) = (3x² - 3x - 18)/(x² - 4)

X – intercepts occurs when y = 0.

f(0) = (3x² – 3x - 18)/(x² - 4)

x - 3 = 0

x = 3

So, the x – intercepts is 3.

Horizontal asymptote :

f(x) = (3x² - 3x - 18)/(x² - 4)

degree of numerator = degree of denominator

y = leading coefficient of N(x)/leading coefficient of D(x).

= 3/1

So, equation of the horizontal asymptote is y = 3.

Domain :

When x² - 4 = 0

(x + 2) (x – 2) = 0

x + 2 = 0 and x – 2 = 0

x = -2 x = 2

So, all real values except -2 and 2.

Example 3 :

f(x) = (x² + 6x + 8)/(x² + 3x - 4)

Solution :

Discontinuity :

f(x) = (x² + 6x + 8)/(x² + 3x - 4)

By factoring,

x² + 6x + 8 = (x + 2) (x + 4)

x² + 3x – 4 = (x + 4) (x – 1)

f(x) = (x + 2) (x+ 4)/((x + 4) (x – 1)

x + 4 = 0 and x – 1 = 0

x = -4 x = 1

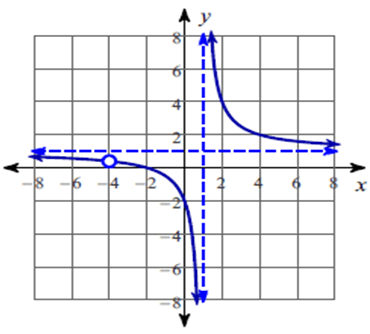
The function is discontinuous at x = -4 and x = 1.

Holes :

x + 4 = 0

x = -4

So, there is a hole at x = -4.

Vertical asymptote :

x – 1 = 0

x = 1

So, the vertical asymptotes at x = 1.

X – intercepts :

f(x) = (x + 2) (x + 4)/(x + 4) (x – 1)

X – intercepts occurs when y = 0.

0 = (x + 2)/(x – 1)

x + 2 = 0

x = -2

So, the x – intercepts is -2.

Horizontal asymptote :

f(x) = (x² + 6x + 8)/(x² + 3x - 4)

degree of numerator = degree of denominator

y = leading coefficient of N(x)/leading coefficient of D(x).

So, equation of the horizontal asymptote is y = 1.

Domain :

When x + 4 = 0 and x - 1 = 0

x = -4 and x = 1

So, all real values except -4 and 1.

Example 4 :

f(x) = (2x + 6)/(x² + 5x + 6)

Solution :

Discontinuity :

f(x) = (2x + 6)/(x² + 5x + 6)

2x + 6 = 2(x + 3)

By factoring,

x² + 5x + 6 = (x + 3) (x + 2)

f(x) = 2(x + 3)/(x + 3) (x + 2)

x + 3 = 0 and x + 2 = 0

x = -3 and x = -2

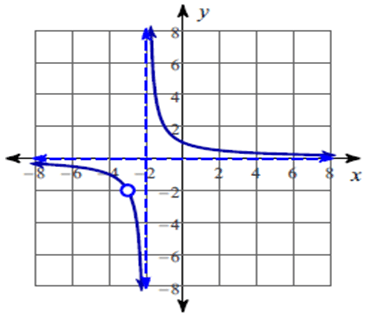
The function is discontinuous at x = -2 and x = -3.

Holes :

x + 3 = 0

x = -3

So, there is a hole at x = -3.

Vertical asymptote :

x + 2 = 0

x = -2

So, the vertical asymptotes at x = -2.

X – intercepts :

f(x) = 2(x + 3)/(x + 3) (x + 2)

X – intercepts occurs when y = 0.

f(0) = 2/(x + 2)

= 0

So, the x – intercepts is none.

Horizontal asymptote :

f(x) = (2x + 6)/(x² + 5x + 6)

degree of numerator < degree of denominator

So, equation of the horizontal asymptote is y = 0 which is the x – axis.

Domain :

When x + 3 = 0 and x + 2 = 0

x = -3 and x = -2

So, all real values except -3 and -2.

Example 5 :

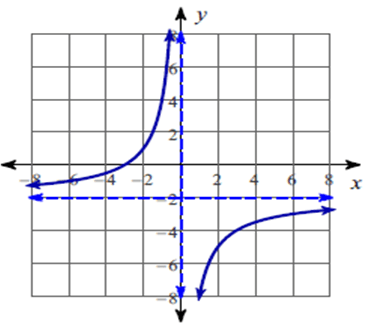
f(x) = (-2x - 6)/x

Solution :

Discontinuity :

f(x) = (-2x - 6)/x

The function is discontinuous at x = 0.

Holes :

None

Vertical asymptote :

f(x) = (-2x - 6)/x

So, the vertical asymptotes at x = 0.

X – intercepts :

f(x) = (-2x - 6)/x

= -2(x + 3)/x

X – intercepts occurs when y = 0.

f(0) = -2(x + 3)/x

x + 3 = 0

x = -3

So, the x – intercepts is -3.

Horizontal asymptote :

f(x) = (-2x - 6)/x

degree of numerator = degree of denominator

y = leading coefficient of N(x)/leading coefficient of D(x).

= -2/1

So, equation of the horizontal asymptote is y = -2.

Domain :

When x = 0

So, all real values except 0.

Example 6 :

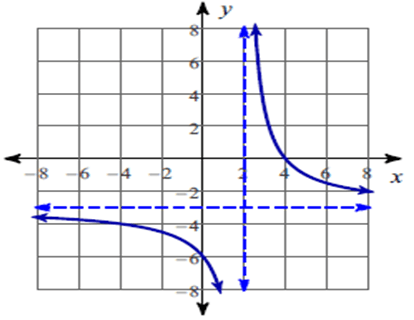
f(x) = (-3x + 12)/(x – 2)

Solution :

Discontinuity :

f(x) = (-3x + 12)/(x – 2)

x – 2 = 0

x = 2

The function is discontinuous at x = 2.

Holes :

None

Vertical asymptote :

x – 2 = 0

x = 2

So, the vertical asymptote at x = 2.

X – intercepts :

f(x) = (-3x + 12)/(x – 2)

= -3(x - 4)/(x – 2)

X – intercepts occurs when y = 0.

f(0) = -3(x - 4)/(x – 2)

x - 4 = 0

x = 4

So, the x – intercepts is 4.

Horizontal asymptote :

f(x) = (-3x + 12)/(x – 2)

degree of numerator = degree of denominator

y = leading coefficient of N(x)/leading coefficient of D(x).

= -3/1

So, equation of the horizontal asymptote is y = -3.

Domain :

When x – 2 = 0

x = 2

So, all real values except 2