GRAPHING QUADRATIC FUNCTIONS IN VERTEX FORM

Graph the following function.

Problem 1 :

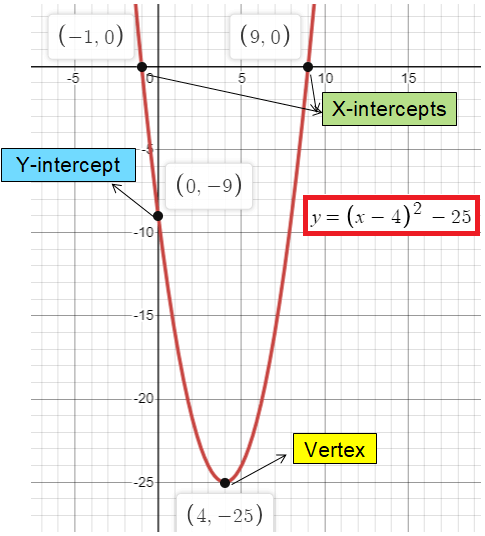
y = (x - 4)² - 25

Solution :

Finding vertex :

y = (x - 4)² - 25

By comparing the given equation with vertex form

y = a(x - h)² + k

we get (h, k) ==> (4, -25)

The vertex is at (4, -25).

Here a = 1 > 0, then the parabola opens up. It will have minimum.

Finding x-intercepts :

0 = (x - 4)² - 25

(x - 4)² = 25

x - 4 = √25

x - 4 = ±5

x-intercepts are (-1, 0) and (9, 0).

Finding y-intercept :

Put x = 0

y = (0 - 4)² - 25

y = 16 - 25

y = -9

y-intercept is (0, -9)

Problem 2 :

y = (-1/2)(x + 3)² + 8

Solution :

Finding vertex :

y = (-1/2)(x + 3)² + 8

By comparing the given equation with vertex form

y = a(x - h)² + k

we get (h, k) ==> (-3, 8)

The vertex is at (-3, 8).

Here a = -1/2 < 0, then the parabola opens down. It will have maximum.

Finding x-intercepts :

0 = (-1/2)(x + 3)² + 8

(-1/2)(x + 3)² + 8 = 0

(-1/2)(x + 3)² = -8

Multiplying by 2 on both sides, we get

(x + 3)² = 16

x + 3 = √16

x + 3 = ±4

x-intercepts are (1, 0) and (-7, 0).

Finding y-intercept :

Put x = 0

y = (-1/2)(0 + 3)² + 8

y = -9/2 + 8

y = (-9+16)/2

y = 7/2

y-intercept is (0, 7/2)

Problem 3 :

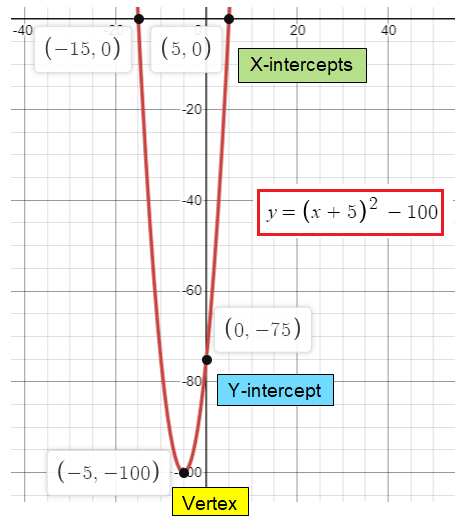
y = (x + 5)² - 100

Solution :

Finding vertex :

y = (x + 5)² - 100

By comparing the given equation with vertex form

y = a(x - h)² + k

we get (h, k) ==> (-5, -100)

The vertex is at (-5, -100).

Here a = 1 > 0, then the parabola opens up. It will have minimum.

Finding x-intercepts :

0 = (x + 5)² - 100

(x + 5)² - 100 = 0.

(x + 5)² = 100

x + 5 = √100

x + 5 = ±10

x-intercepts are (5, 0) and (-15, 0).

Finding y-intercept :

Put x = 0

y =  (0 + 5)² - 100

y = 25 - 100

y = -75

y-intercept is (0, -75)

Problem 4 :

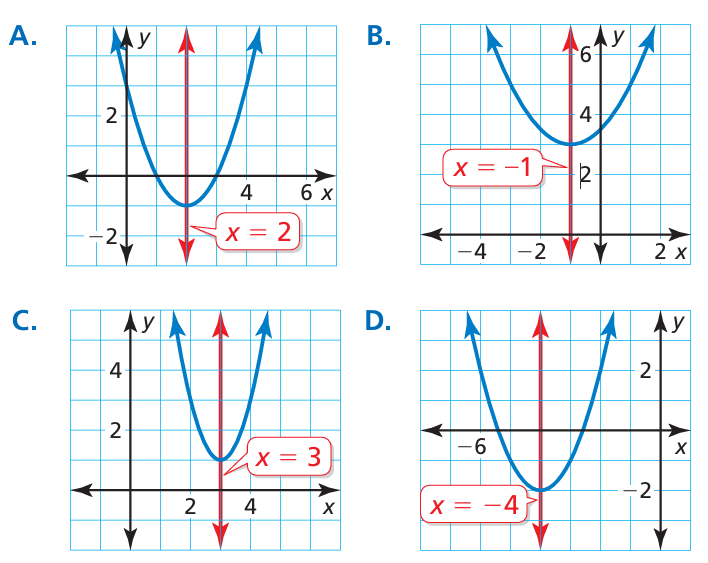
Use the axis of symmetry to match the equation with its graph.

a)  y = 2(x − 3)² + 1

b)  y = (x + 4)² − 2

c)  y = 1/2 (x + 1)² + 3

d) y = (x − 2)² − 1

Solution :

By comparing the above functions with y = a(x - h)² + k, we get the vertex in the form of (h, k).

Equation of axis of symmetry is x = h

a)  y = 2(x − 3)² + 1

we get h = 3 and k = 1

Equation of axis of symmetery x = 3

Option C is correct.

b)  y = (x + 4)² − 2

y = (x - (-4))² − 2

we get h = -4 and k = -2

Equation of axis of symmetery x = -4

Option D is correct.

c)  y = 1/2 (x + 1)² + 3

y = 1/2(x - (-1))² + 3

we get h = -1 and k = 3

Equation of axis of symmetery x = -1

Option B is correct.

d) y = (x − 2)² − 1

we get h = 2 and k = -1

Equation of axis of symmetery x = 2

Option A is correct.

Problem 5 :

Two quadratic functions have graphs with vertices (2, 4) and (2, −3). Explain why you can not use the axes of symmetry to distinguish between the two functions.

Solution :

Axis of symmetry for the first function which has the vertex of (2, 4).

Equation of axis of symmetery :

x = 2

Axis of symmetry for the second function which has the vertex of (2, -3).

Equation of axis of symmetery :

x = 2

Equation of axis of symmetry for both functions they are the same, so you cannot differentiate these two functions.

Problem 6 :

A quadratic function is increasing to the left of x = 2 and decreasing to the right of x = 2. Will the vertex be the highest or lowest point on the graph of the parabola? Explain.

Solution :

The graph changes from increasing to decreasing, then it must have highest point on the parabola.