GRAPHING PROPORTIONAL RELATIONSHIPS
What do we notice about proportional relationships ?
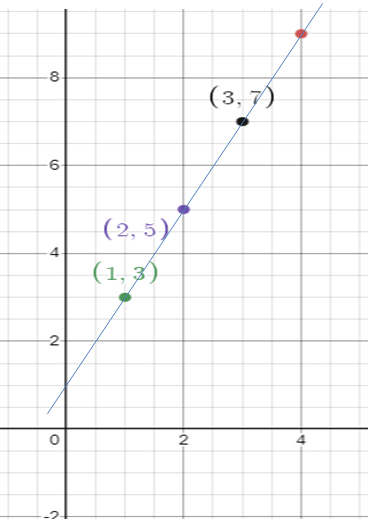
The graph of a proportional relationships is a straight line that passes through the origin.
The constant of proportionality is always the point (x, k f(x)) where k is the constant of proportionality. Additionally, you can find the constant of proportionality by finding the ratio of y/x for any point on the line.
Determine if the relationship shown in the table is proportional. Then each graph in the coordinate plane and connect with a straight line. Find the following.
i) Check if the relation is proportional
ii) Constant of proportionality
iii) Equation
Problem 1 :
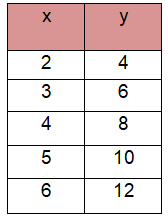
Solution :
i) Check if the relation is proportional
k = y/x
|
k = 4/2 k = 2 |
k = 6/3 k = 2 |
k = 8/4 k = 2 |
k = 10/5 k = 2 |
Since the value of k is the same, then the given relation represents proportional relationship.
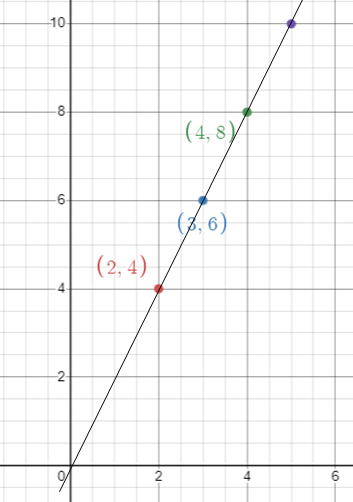
ii) Constant of proportionality
k = 2
iii) Equation
y = kx
y = 2x
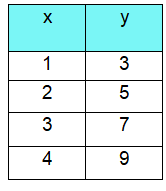
Problem 2 :
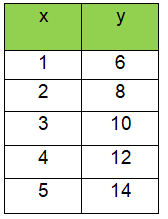
Solution :
|
k = 6/1 k = 6 |
k = 8/2 k = 4 |
k = 10/3 k = 10/3 |
k = 12/4 k = 3 |
Since the value of k is not same, then the given relation does mot represents proportional relationship.
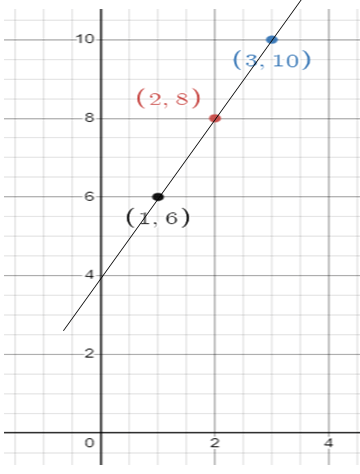
ii) Constant of proportionality
doesn't have
Problem 3 :
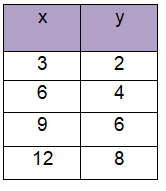
Solution :
|
k = 2/3 k = 2/3 |
k = 4/6 k = 2/3 |
k = 6/9 k = 2/3 |
k = 8/12 k = 2/3 |
Since the value of k is the same, then the given relation represents proportional relationship.
ii) Constant of proportionality
k = 2/3
iii) Equation
y = kx
y = (2/3)x
Problem 4 :
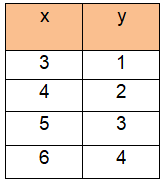
Solution :
|
k = 1/3 k = 1/3 |
k = 2/4 k = 1/2 |
k = 3/5 k = 3/5 |
k = 4/6 k = 2/3 |
Since the value of k is not the same, then the given relation does not represent proportional relationship.
It is non proportional relationship.
Problem 5 :
The cost of renting video games from games Inc is shown in the table. Determine whether the cost is proportional to the number of games rented by graphing on the coordinate plane.
Solution :
The cost of video games does not represent a proportional relationship.
Problem 6 :
The slowest mammal on the earth is the tree sloth. It moves at a rate of 6 feet per minute. Determine whether the number of feet of sloth moves is proportional to the number of minutes it moves by graphing on the coordinate plane.
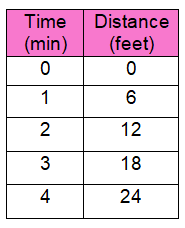
Solution :
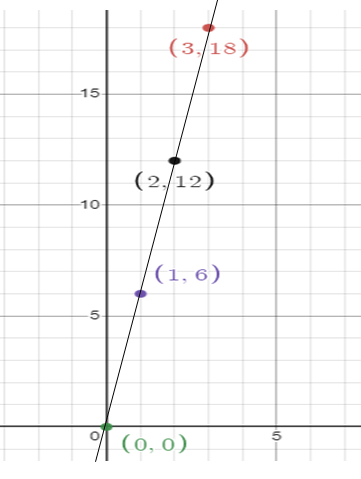
Since it passes through (0, 0), it is a proportional relationship.
Problem 7 :
Identify the constant of proportionality from the graph given below.
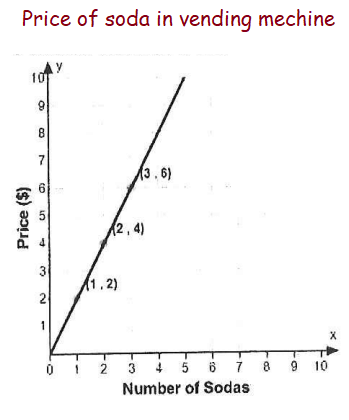
Solution :
Constant of proportionality = y/x
From (1, 2)
k = 2/1
k = 2
So, the constant of proportionality is 2.
Problem 8 :
Find the constant of proportionality.
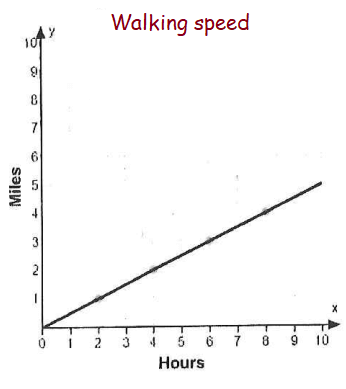
Solution :
Constant of proportionality = y/x
From (2, 1)
k = 1/2
So, the constant of proportionality is 1/2.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling