GRAPHING PIECEWISE FUNCTIONS

A piecewise function is a function defined by two or more equations. Each “piece” of the function applies to a different part of its domain. An example is shown below.

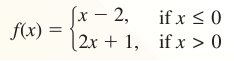
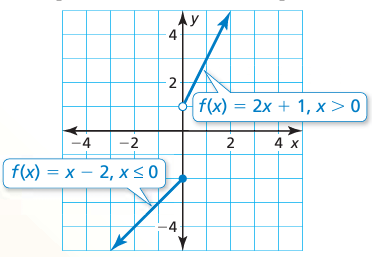
• The expression x − 2 represents the value of f when x is less than or equal to 0.
• The expression 2x + 1 represents the value of f when x is greater than 0.

Carefully graph each of the following. Identify whether or not the graph is a function. Then, evaluate the graph at any specified domain value. You may use your calculators to help you graph, but you must sketch it carefully.

Problem 1 :

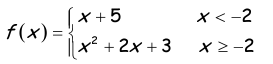
i) Check if the graph is a function or not.

ii)  Evaluate

a) f(3)     b) f(-4)      c) f(-2)

Solution :

Graphing Line :

Graphing y = x + 5, where x < -2

Since it is linear, we can compare the given with y = mx + b, slope = 1 and y-intercept = 5. It must be a raising line with y-intercept of 5

Domain of the line is (- ∞, 2)

Graphing parabola :

Converting x² + 2x + 3 into vertex form,

= x² + 2x + 3

= x² + 2 x (1) + 1² - 1² + 3

= (x + 1)² - 1 + 3

= (x + 1)² + 2

(h, k ) ==> (-1, 2)

Domain of the parabola is [2, ∞).

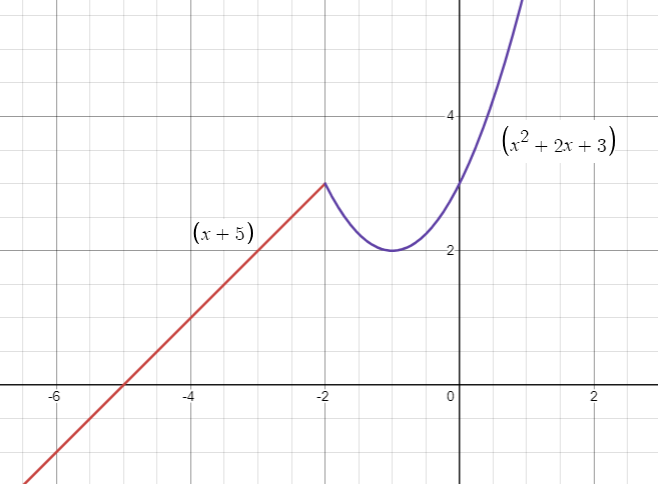
i) Drawing the vertical line through the graph, the line will intersect the graph maximum once. So, it is a function.

ii)  a) f(3) :

x = 3 it satisfies the condition ≥ -2

f(x) = x² + 2x + 3

f(-3) = (-3)² + 2(-3) + 3

= 9 - 6 + 3

= 12 - 6

= 6

b) f(-4) :

x = -4 it satisfies the condition < -2

f(x) = x + 5

f(-4) = -4 + 5

= 1

c) f(-2) :

x = -2, it satisfies the condition ≥ -2

f(x) = x² + 2x + 3

f(-2) = (-2)² + 2(-2) + 3

= 4 - 4 + 3

f(-2) = 3

Problem 2 :

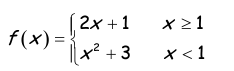
i) Check if the graph is a function or not.

ii)  Evaluate

a) f(-2)     b) f(6)      c) f(1)

Solution :

Graphing Line :

y = 2x + 1

Slope = 2 and y-intercept = 1

x-intercept, put y = 0

2x + 1 = 0

2x = -1

x = -1/2

Domain of line is [1, ∞).

Graphing parabola :

y = x² + 3

Vertex form :

y = (x - 0)² + 3

Vertex (h, k) ==> (0, 3)

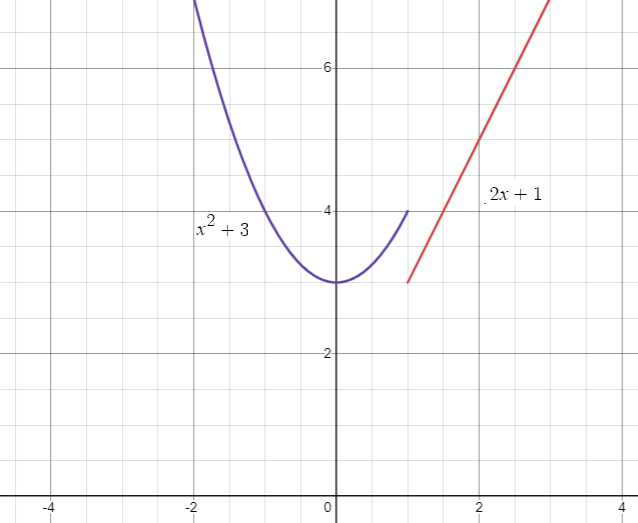
Domain of parabola is -(∞, 1).

i) Using vertical line test, it is a function.

ii)  

a) f(-2) :

Here x = -2, which satisfies the condition x < 1

f(x) =  x² + 3

f(-2) =  (-2)² + 3

= 4 + 3

= 7

b) f(6)

Here x = 6, which satisfies the condition x ≥ 1

f(x) =  2x + 1

f(6) = 2(6) + 1

= 12 + 1

= 13

c) f(1)

Here x = 1, which satisfies the condition x ≥ 1

f(x) =  2x + 1

f(1) = 2(1) + 1

= 3

Problem 3 :

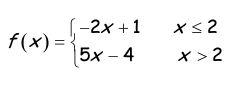
i) Check if the graph is a function or not.

ii)  Evaluate

a) f(-4)     b) f(8)      c) f(2)

Solution :

Graphing first line :

y = -2x + 1

Slope = -2 and y-intercept = 1

It is a falling line with slope -2.

Graphing second line :

y = 5x - 4

Slope = 5 and y-intercept = -4

Since the domain is > 2, then we cannot mark the y-intercept.

It is a raising line with slope 5.

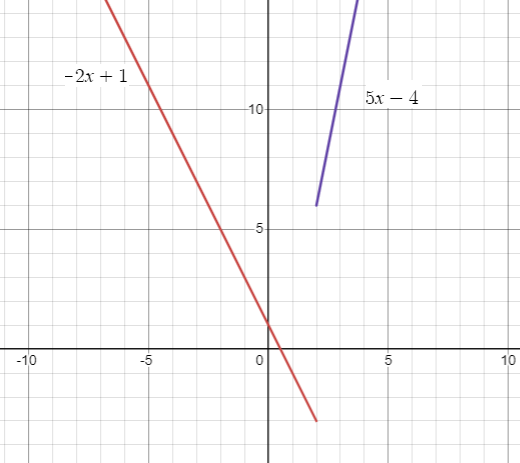
ii)

a) f(-4)

Here x = -4 satisfying the condition x ≤ 2

f(x) = -2x + 1

f(-4) = -2(-4) + 1

= 8 + 1

f(-4) = 9

b) f(8)

Here x = 8 satisfying the condition x > 2

f(x) = 5x - 4

f(8) = 5(8) - 4

= 40 - 4

f(8) = 36

c) f(2)

Here x = 2 satisfying the condition x ≤ 2

f(x) = -2x + 1

f(2) = -2(2) + 1

= -4 + 1

f(2) = -3

Problem 4 :

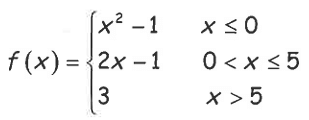
Solution :

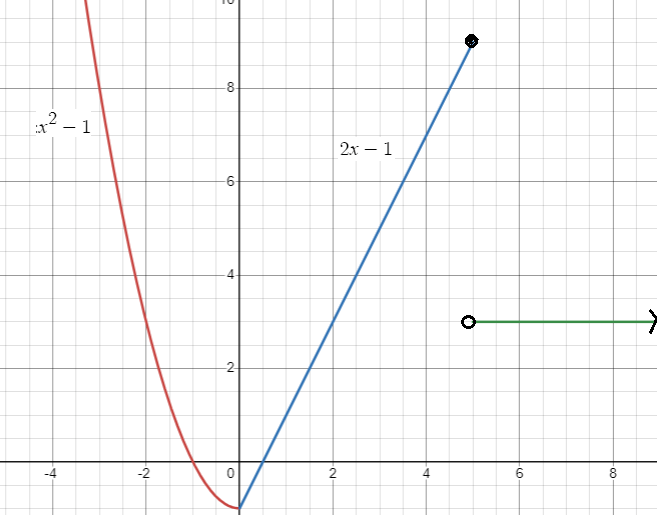
Graphing first piece :

f(x) = x² - 1

Writing in the vertex form, we get

f(x) = (x - 0)² - 1

Here the vertex is (0, -1).

Graphing second piece :

f(x) = 2x - 1

It is a straight line, with slope = 2 and y-intercept = -1

At x = 5, we have to draw the filled circle.

Graphing third piece :

f(x) = 3

Put the filled circle.

At 5, we have to draw the unfilled circle and continue drawing line.