GRAPHING LOGARITHMIC FUNCTIONS EXAMPLES

Graph each of the following logarithmic functions. Label the key point for each.

Problem 1 :

f(x) = log₂x

Solution:

f(x) = log₂x

Finding points :

If x = 2, f(2) = log₂2

f(2) = 1

If x = 4, f(4) = log₂4

f(4) = 2

If x = 8, f(8) = log₂8

f(8) = 3

So, the points are (2, 1) (4, 2) and (8, 3).

Finding x and y-intercepts :

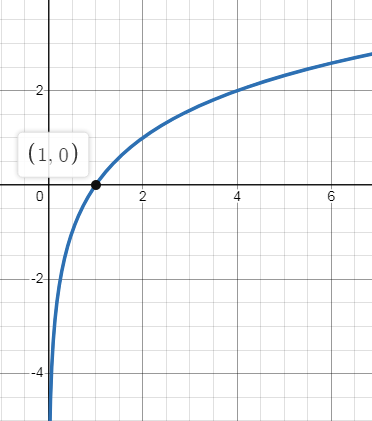
Hence, f(x) = log₂x graph cut x-axis at (1, 0).

Problem 2 :

f(x) = log₄x

Solution:

Finding points :

f(x) = log₄x

If x = 2, f(2) = log₄2

f(2) = 0.5

If x = 4, f(4) = log₄4

f(4) = 1

If x = 8, f(8) = log₄8

f(8) = 1.5

So, the points are (2, 0.5) (4,1) and (8, 1.5).

Finding x and y-intercepts :

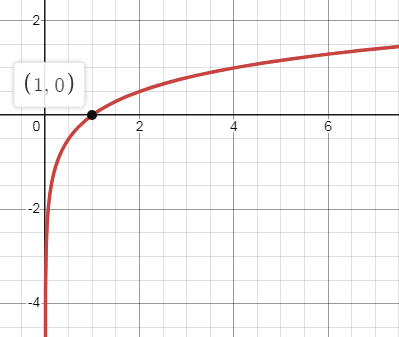
Hence, f(x) = log₄x graph cut x-axis at (1, 0).

Problem 3 :

f(x) = log₄(x - 3)

Solution:

Finding points :

f(x) = log₄(x - 3)

If x = 4, f(4) = log₄(4 - 3)

 = log₄1

f(4) = 0

If x = 5, f(5) = log₄(5 - 3)

= log₄(2)

f(5) = 0.5

If x = 7, f(7) = log₄(7 - 3)

= log₄(4)

f(7) = 1

So, the points are (4, 0) (5, 0.5) and (7, 1).

Finding x and y -intercepts :

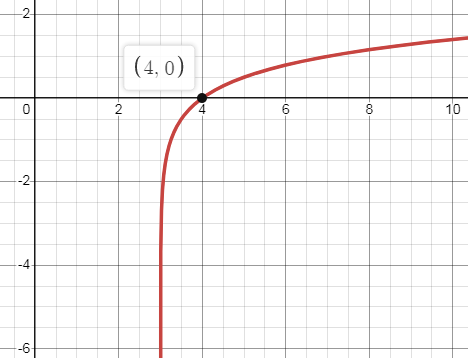
Hence, f(x) = log₄(x - 3) graph cut x-axis at (4, 0).

Problem 4 :

f(x) = log₂(x + 2)

Solution:

f(x) = log₂(x + 2)

Finding points :

If x = -1, f(-1) = log₂(-1 + 2)

= log₂(1)

f(-1) = 0

If x = 2, f(2) = log₂(2 + 2)

= log₂(4)

f(2) = 2

If x = 6, f(6) = log₂(6 + 2)

= log₂(8)

f(8) = 3

So, the points are (-1, 0) (2, 2) and (8, 3).

Finding x and y-intercepts :

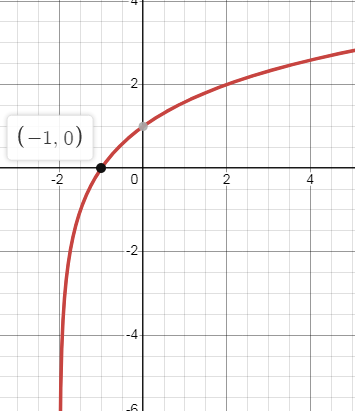
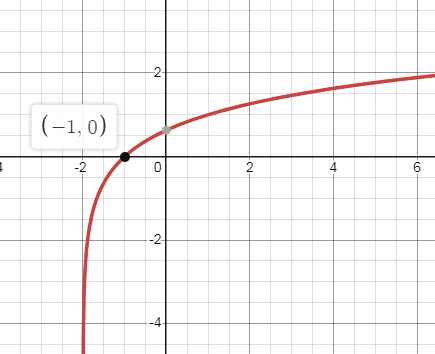
Problem 5 :

f(x) = log₃(x + 2)

Solution:

f(x) = log₃(x + 2)

Finding points :

If x = 1, f(1) = log₃(1 + 2)

= log₃(3)

f(1) = 1

If x = 2, f(2) = log₃(2 + 2)

= log₃(4)

f(2) = 1.2

If x = 3, f(3) = log₃(3 + 2)

= log₃(5)

f(3) = 1.5

So, the points are (1, 1) (2, 1.2) and (3, 1.5).

Finding x and y-intercepts :

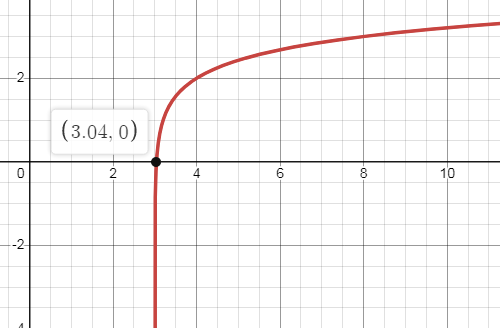
Problem 6 :

f(x) = log₅(x - 3) + 2

Solution:

f(x) = log₅(x - 3) + 2

Finding points :

If x = 4, f(4) = log₅(4 - 3) + 2

= log₅(1) + 2

f(4) = 2

If x = 8, f(8) = log₅(8 - 3) + 2

= log₅(5) + 2

f(8) = 3

If x = 10, f(10) = log₅(10 - 3) + 2

= log₅(7) + 2

f(10) = 3.2

So, the points are (4, 2) (8, 3) and (10, 3.2)