GRAPHING LINES USING INTERCEPTS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
To find x and y-intercept of a line, we have two ways.
Method 1 :
(i) To find x-intercept, apply y = 0. Then write the coordinate as (x, 0).
(ii) To find y-intercept, apply x = 0. Then write the coordinate as (0, y).
Method 2 :
Convert the equation from standard form to intercept form.
(x/a) + (y/b) = 1
a = x-intercept and b = y-intercept
After finding x and y-intercepts, we can mark the points in the form (x, 0) and (0, y).
Find the x and y intercept of the line with the given equation.
Problem 1 :
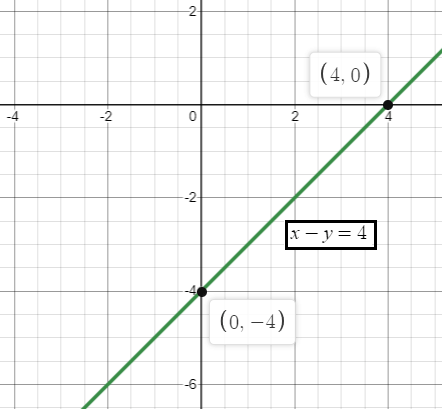
x - y = 4
Solution :
|
x-intercept : Put y = 0 x - 0 = 4 x = 4 |
y-intercept : Put x = 0 0 - y = 4 y = -4 |
To find x
and y intercept we have to compare given equation with intercept form
(x/a) + (y/b) = 1
x - y = 4
Dividing by 4 on both sides,
x/4 - y/4 = 4/4
(x/4) - (y/4) = 1
x -intercept (a) = 4
y -intercept (b) = - 4
The required points are (4, 0) and (0, -4).
Problem 2 :
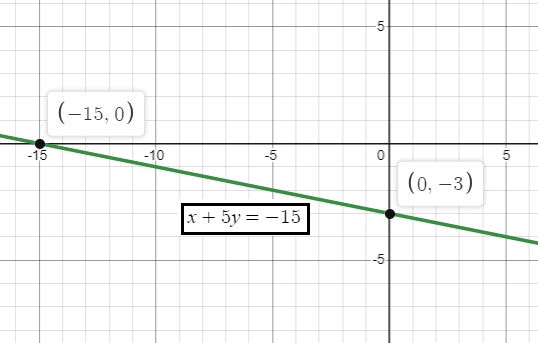
x + 5y = -15
Solution :
To find x and y intercept we have to compare given equation with intercept form
(x/a) + (y/b) = 1
x + 5y = -15
Dividing by -15 on both sides,
(x/-15) + (5y/-15) = -15/-15
(x/-15) + (y/-3) = 1
x -intercept (a) = - 15
y -intercept (b) = - 3
So, the points are (-15, 0) and (0, -3).
Problem 3 :
3x - 4y = -12
Solution :
To find x and y intercept we have to compare given equation with intercept form
(x/a) + (y/b) = 1
3x - 4y = -12
Dividing by -12 on both sides,
(3x/-12) - (4y/-12) = -12/-12
(x/-4) - (y/-3) = 1
x -intercept (a) = - 4
y -intercept (b) = 3
So, the points are (-4, 0) and (0, 3).
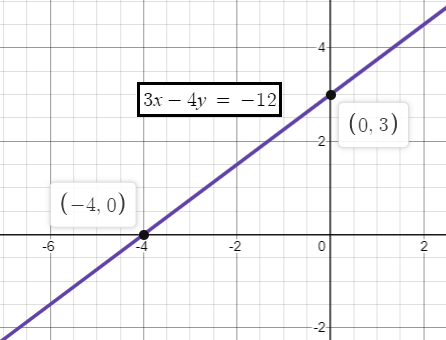
Problem 4 :
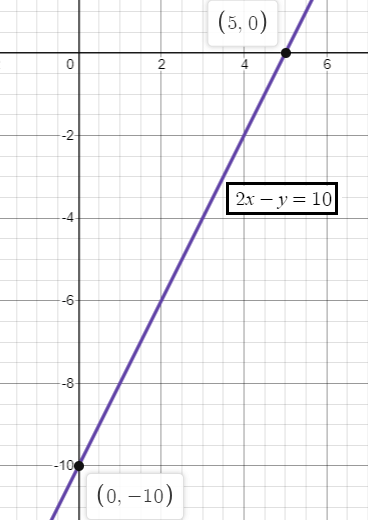
2x - y = 10
Solution :
To find x and y intercept we have to compare given equation with intercept form
(x/a) + (y/b) = 1
2x - y = 10
Dividing by 10 on both sides,
(2x/10) - (y/10) = 10/10
(x/5) - (y/10) = 1
x -intercept (a) = 5
y -intercept (b) = - 10
So, the points are (5, 0) and (0, -10).
Problem 5 :
4x - 5y = 20
Solution :
To find x and y intercept we have to compare given equation with intercept form
(x/a) + (y/b) = 1
4x - 5y = 20
Dividing by 20 on both sides,
(4x/20) - (5y/20) = 20/20
(x/5) - (y/4) = 1
x -intercept (a) = 5
y -intercept (b) = -4
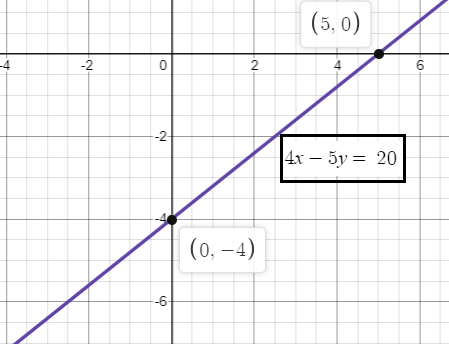
Problem 6 :
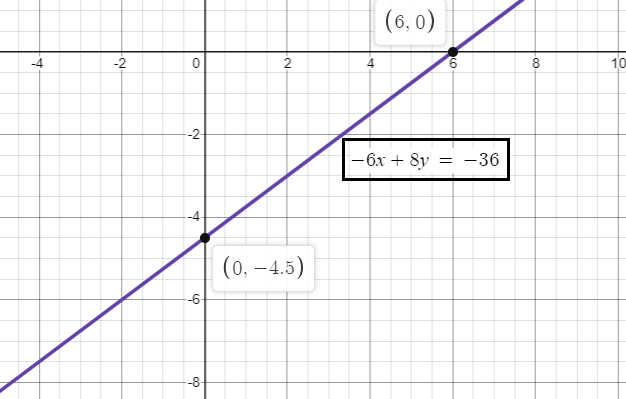
-6x + 8y = -36
Solution :
To find x and y intercept we have to compare given equation with intercept form
(x/a) + (y/b) = 1
-6x + 8y = -36
Dividing by -36 on both sides,
(-6x/-36) + (8y/-36) = -36/-36
(x/6) + (2y/-9) = 1
x -intercept (a) = 6
y -intercept (b) = - 9/2
Problem 7 :
You are ordering shirts for the math club at your school. Short-sleeved shirts cost $10 each. Long-sleeved shirts cost $12 each. You have a budget of $300 for the shirts. The equation 10x + 12y = 300 models the total cost, where x is the number of short-sleeved shirts and y is the number of long-sleeved shirts.
a. Graph the equation. Interpret the intercepts.
b. Twelve students decide they want short-sleeved shirts. How many long-sleeved shirts can you order?
Solution :
10x + 12y = 300
a)
|
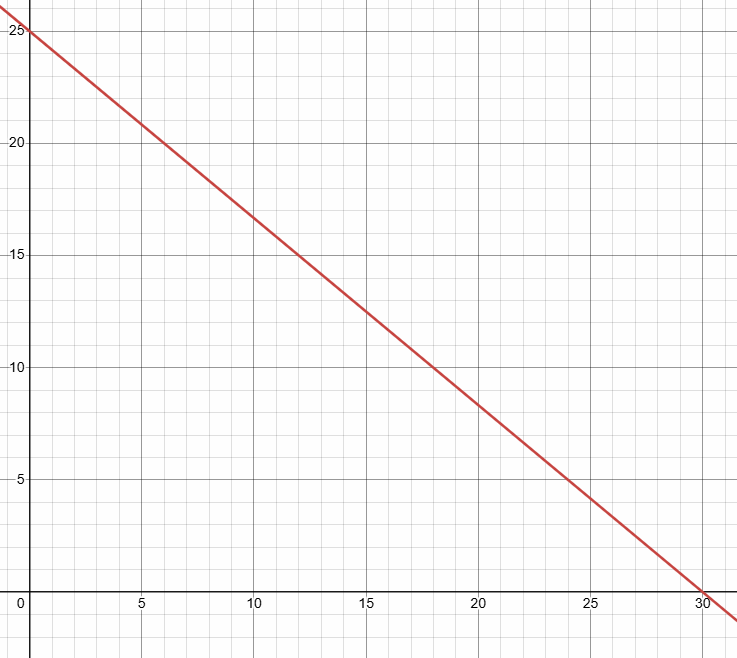
When x = 0 12y = 300 y = 300/12 y = 25 |
When y = 0 10x = 300 x = 300/10 x = 30 |
- Maximum number of short sleeved dress they can order is 30
- Maximum number of long sleeved dress they can order is 25.
b) When x = 12
10(12) + 12y = 300
120 + 12y = 300
12y = 300 - 120
12y = 180
y = 180/12
y = 15
Number of long sleeved shirts they can order is 15.
Problem 8 :
You lose track of how many 2-point baskets and 3-point baskets a team makes in a basketball game. The team misses all the 1-point baskets and still scores 54 points. The equation 2x + 3y = 54 models the total points scored, where x is the number of 2-point baskets made and y is the number of 3-point baskets made.
a. Find and interpret the intercepts.
b. Can the number of 3-point baskets made be odd? Explain your reasoning.
c. Graph the equation. Find two more possible solutions in the context of the problem.
Solution :
2x + 3y = 54
a) 2x + 3y = 54
|
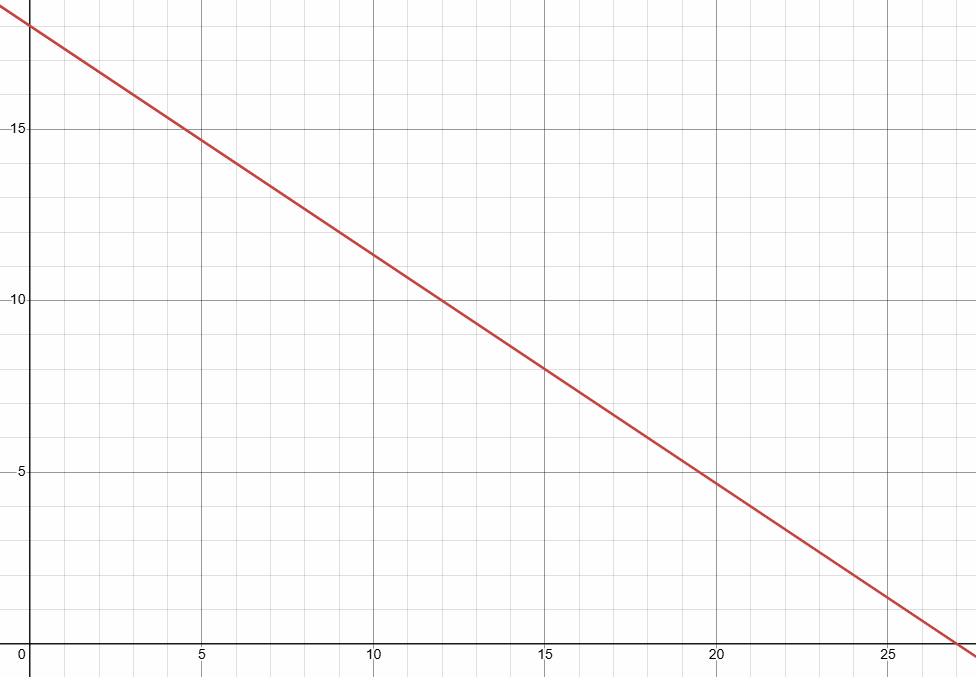
When x = 0 3y = 54 y = 54/3 y = 18 |
When y = 01 2x = 54 x = 54/2 x = 27 |
Maximum number of 2-point baskets you may loose is 27
Maximum number of 3 point baskets you may loose is 18.
b) For the product 3y be even, y must be an even number. So, the number of 3 point baskets made cannot be odd.
c)
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling