GRAPHING LINES IN DIFFERENT FORMS
There are different ways to find graph of the linear equation.
(i) Apply some random values of x, from that we can find out the value of y. Write them as coordinates and plotting in the graph, we will get graph.
Graph the equation using any method.
Problem 1 :
6y = 3x + 6
Solution :
6y = 3x + 6
Divide each side by 6.
y = (3/6) x + (6/6)
y = (1/2) x + 1
The above equation is in the form y = mx + b
Then,
Slope (m) = 1/2
y-intercept = 1
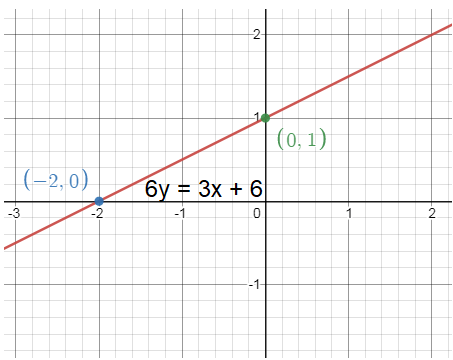
Problem 2 :
-3 + x = 0
Solution :
-3 + x = 0
x = 3
Since x = 3 is a vertical line, there is no y-intercept and the slope is undefined.
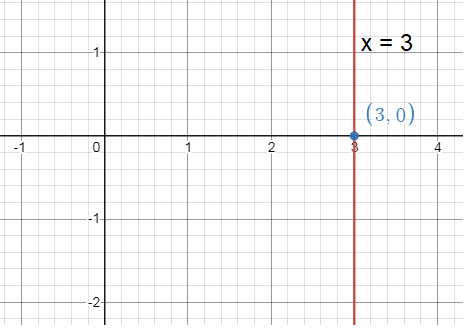
Problem 3 :
4y = 16
Solution :
y = 4
y = 0x + 4
The above equation is in the form y = mx + b
Then,
Slope (m) = 0
y-intercept = 4
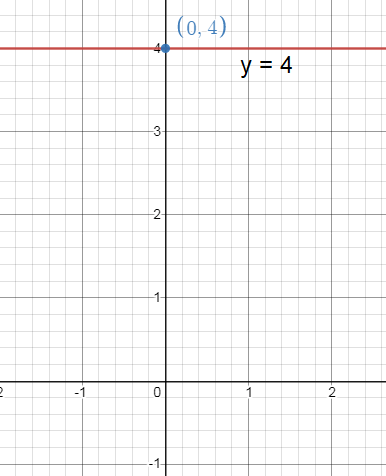
Problem 4 :
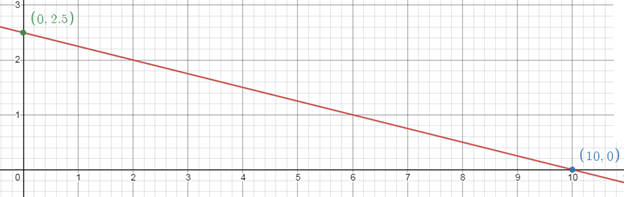
8y = -2x + 20
Solution :
To find x and y intercept we have to compare given equation with intercept form (x/a) + (y/b) = 1
2x + 8y = 20
Dividing by 20 on both sides,
(2x/20) + (8y/20) = 1
(x/10) + (2y/5) = 1
x -intercept (a) = 10
y -intercept (b) = 5/2
Problem 5 :
-4x = 8y + 12
Solution :
8y = -4x - 12
Divide each side by 8.
y = (-4/8) x - (12/8)
y = (-1/2) x - (3/2)
The above equation is in the form y = mx + b
Then,
Slope (m) = -1/2
y-intercept = -3/2
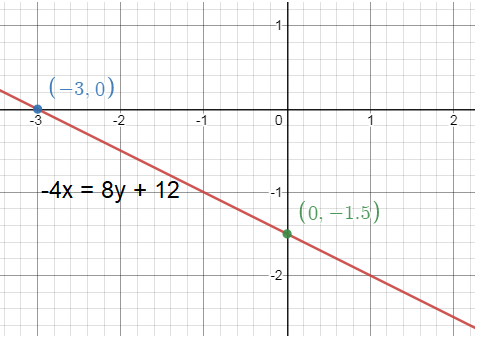
Problem 6 :
3.5x = 10.5
Solution :
3.5x = 10.5
x = 3
Since x = 3 is a vertical line, there is no y-intercept and the slope is undefined.
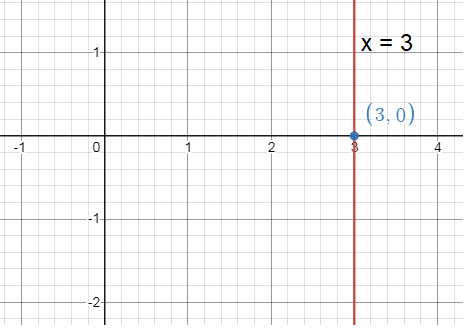
Problem 7 :
14 - 3x = 7y
Solution :
7y = -3x + 14
To find x and y intercept we have to compare given equation with intercept form (x/a) + (y/b) = 1
3x + 7y = 14
Dividing by 14 on both sides,
(3x/14) + (7y/14) = 1
(3x/14) + (y/2) = 1
x-intercept = 14/3
y-intercept = 2
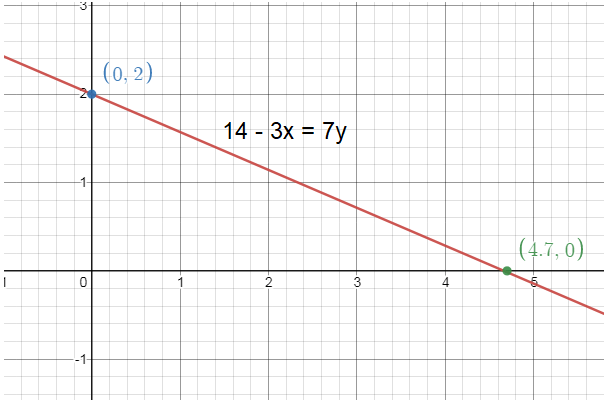
Problem 8 :
2y - 5 = 0
Solution :
2y = 0x + 5
y = 5/2
The above equation is in the form y = mx + b
Then,
Slope (m) = 0
y-intercept = 5/2
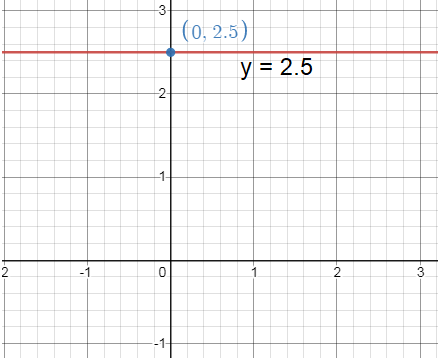
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling