GRAPHING INEQUALITIES IN TWO VARIABLES

To graph inequalities in two variables, we will follow the instruction given below.

Step 1 :

Consider the given inequalities as equations. By finding x and y intercepts, we will get two points on the x and y axis respectively.

Step 2 :

To find x intercept, we put y = 0

To find y intercept, put x = 0

Step 3 :

If we have lesser than or equal to sign ≤, greater than or equal to sign ≥, we have to use solid line to draw the graph.

If we have lesser than sign <, greater than >, we have to use the dotted line to draw the graph.

Step 4 :

Take one point above or below the line and put in the given inequality.

If the given inequality satisfies the point, we can shade that particular region. Other wise shade the opposite region.

Graph the solutions to each of the following inequalities on a separate set of axes.

Problem 1 :

y ≤ 3x + 1

Solution :

y = 3x + 1

x -intercept : y = 0

3x + 1 = 0

3x = -1

x = -1/3

x -intercept: (-1/3, 0)

y -intercept : x = 0

y = 3(0) + 1

y = 0 + 1

y = 1

y -intercept: (0, 1)

Check :

Point (2, -1)

-1 ≤ 3(2) + 1

-1 ≤ 6 + 1

-1 ≤ 7

True

Point (1, -2)

-2 ≤ 3(1) + 1

-2 ≤ 3 + 1

-2 ≤ 4

True

So, we shade the region below the line.

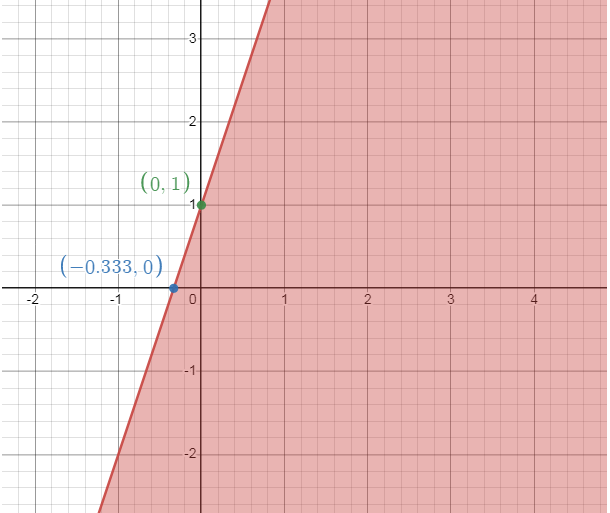
Problem 2 :

y ≥ -2x + 3

Solution :

y = -2x + 3

x -intercept : y = 0

-2x + 3 = 0

-2x = -3

x = 3/2

x -intercept: (3/2, 0)

y -intercept : x = 0

y = -2(0) + 3

y = 3

y -intercept: (0, 3)

Check :

Point (3, 1)

1 ≥ -2(3) + 3

1 ≥ -6 + 3

1 ≥ -3

True

Point (5, 2)

2 ≥ -2(5) + 3

2 ≥ -10 + 3

2 ≥ -7

True

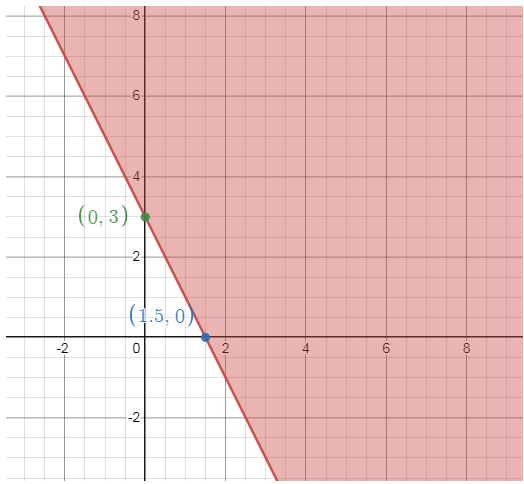
Problem 3 :

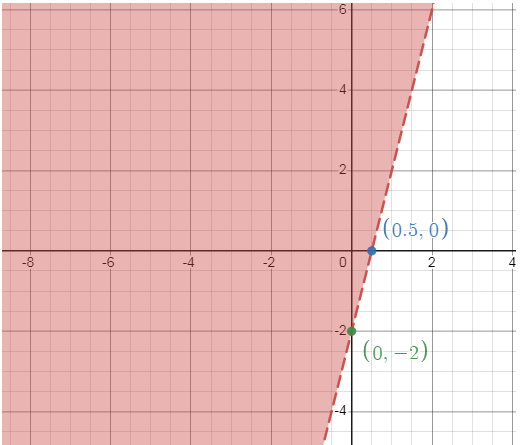
y > 4x - 2

Solution :

y = 4x - 2

x -intercept : y = 0

4x - 2 = 0

4x = 2

x = 1/2

x -intercept: (1/2, 0)

y -intercept : x = 0

y = 4(0) - 2

y = -2

y -intercept: (0, -2)

Check :

Point (-1, 1)

1 > 4(-1) - 2

1 > -4 - 2

1 > -6

True

Point (-2, 5)

5 > 4(-2) - 2

5 > -8 - 2

5 > -10

True

Problem 4 :

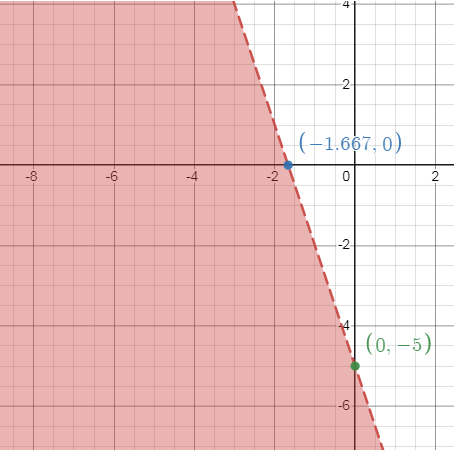
y < -3x - 5

Solution :

y = -3x - 5

x -intercept : y = 0

-3x - 5 = 0

-3x = 5

x = -5/3

x -intercept: (-5/3, 0)

y -intercept : x = 0

y = -3(0) - 5

y = -5

y -intercept is (0, -5)

Check :

Point (-3, -2)

-2 < -3(-3) - 5

-2 < 9 - 5

-2 < 4

True

Point (-5, 1)

1 < -3(-5) - 5

1 < 15 - 5

1 < 10

True

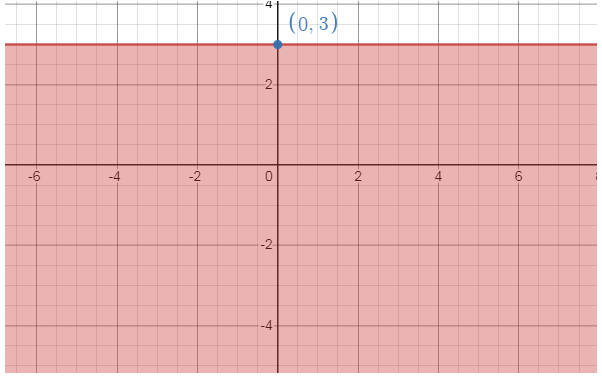
Problem 5 :

y ≤ 3

Solution :

y = 3

y -intercept is (0, 3)

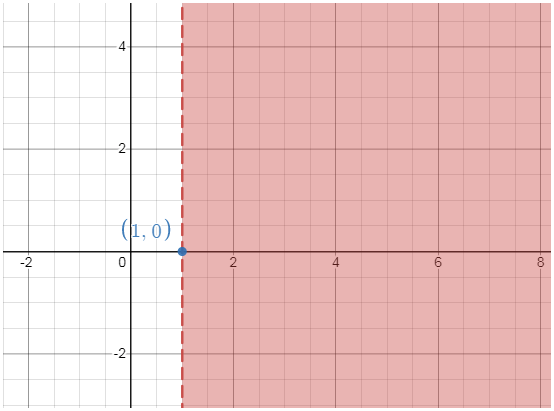
Problem 6 :

x > 1

Solution :

x = 1

x -intercept: (1, 0)

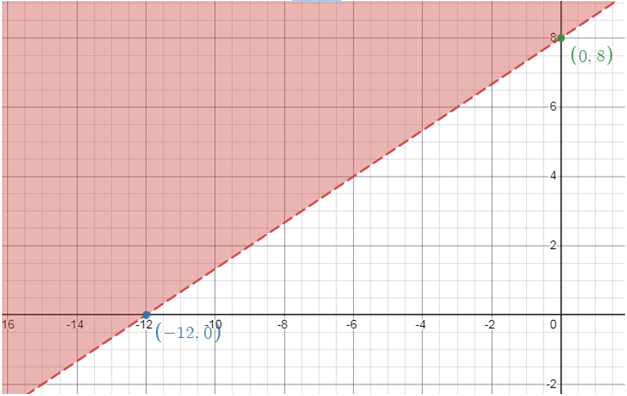
Problem 7 :

y > 2/3x + 8

Solution :

y = 2/3x + 8

x -intercept : y = 0

2/3x + 8 = 0

2/3x = -8

x = -12

x -intercept: (-12, 0)

y -intercept : x = 0

y = 2/3(0) + 8

y = 8

x -intercept: (0, 8)

Check :

Point (-12, 9)

9 > 2/3(-12) + 8

9 > -4 + 8

9 > 4

True

Point (-15, 10)

10 > 2/3(-15) + 8

10 > -10 + 8

10 > -2

True

GRAPHING INEQUALITIES IN TWO VARIABLES

Recent Articles

Finding Range of Values Inequality Problems

Solving Two Step Inequality Word Problems

Exponential Function Context and Data Modeling