GRAPHING EXPONENTIAL FUNCTIONS AND FIND DOMAIN AND RANGE

Graph each function. State the domain and range.

Problem 1 :

f(x) = 2^x

Solution :

Applying some random values for x, we will receive the values of y.

When x = -2, f(-2) = 2^-2  ==> 1/4

When x = -1, f(-1) = 2^-1  ==> 1/2

When x = 0, f(0) = 2⁰  ==> 1

When x = 1, f(1) = 2¹  ==> 2

When x = 2, f(2) = 2²  ==> 4

(-2, 1/4) (-1, 1/2) (0, 1) (1, 2) and (2, 4)

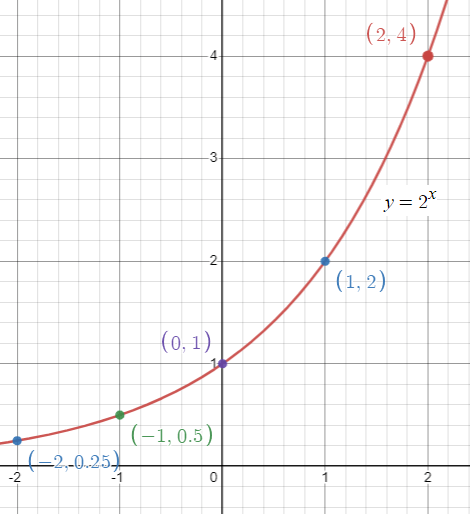
Domain is (-∞, ∞) and range is (0, ∞)

Problem 2 :

f(x) = 2^x+1 + 3

Solution :

Using the concept of transformation, we can draw the graph of the exponential function.

Comparing the given exponential function with general form

f(x) = a b^x-h + k

f(x) = 2^{x - (-1)} + 3

Here h = -1 and k = 3

Horizontally move the graph f(x) = 2^x left 1 unit and vertically move the graph 3 units up.

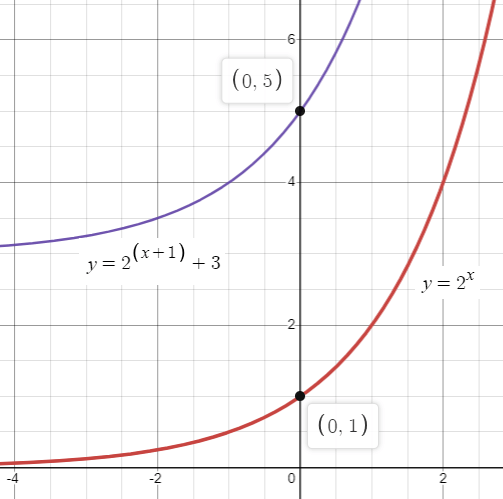
Horizontal asymptote y = 3

Domain is (-∞, ∞) and range is (3, ∞)

Problem 3 :

f(x) = 3^x-2 + 4

Solution :

First let us find the graph of the parent function g(x) = 3^x

Applying some random values for x, we will receive the values of y.

When x = -2, f(-2) = 3^-2  ==> 1/9

When x = -1, f(-1) = 3^-1  ==> 1/3

When x = 0, f(0) = 3⁰  ==> 1

When x = 1, f(1) = 3¹  ==> 3

When x = 2, f(2) = 3²  ==> 9

(-2, 1/9) (-1, 1/3) (0, 1) (1, 3) and (2, 9)

By joining the points, we will get the graph of f(x) = 3^x

Using the concept of transformation, we can draw the graph of the exponential function.

Comparing the given exponential function with general form

f(x) = a b^x-h + k

f(x) = 3^x-2 + 4

Here h = 2 and k = 4

Horizontally move the graph g(x) 2 units right and 4 units up.

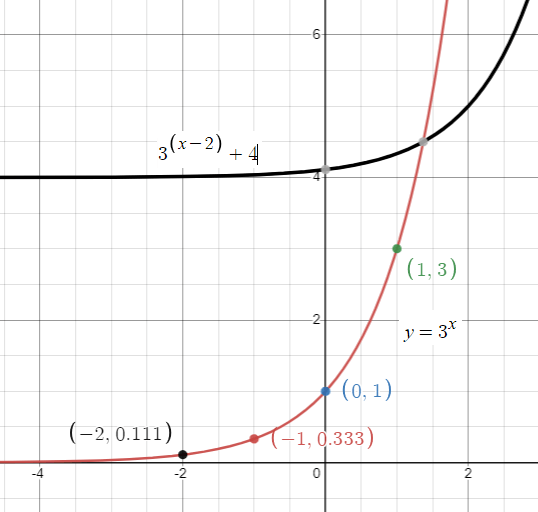
Problem 4 :

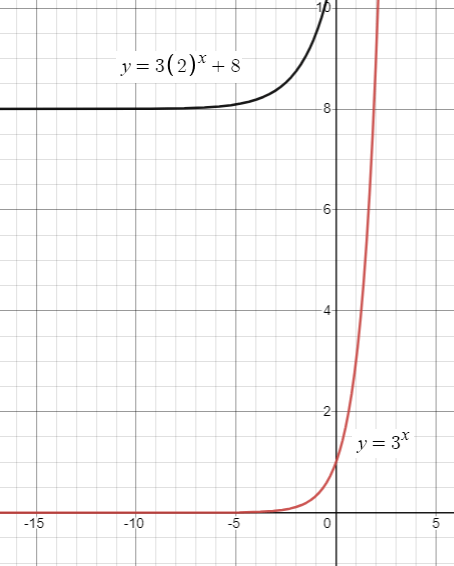
f(x) = 3(2)^x + 8

Solution :

Considering the parent function be g(x) = 2^x

Vertical stretch of 3 units and vertically move the graph 8 units up.

Problem 5 :

The graph of y = (2/3)^x is shown

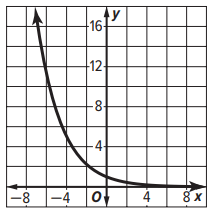
What is the range ?

a)  x ∈ R         b) 0 ≤ y < 1     c)  y ≥ 1      d)  y > 0

Solution :

The given function is decreasing function. The range is y > 0.

Problem 6 :

How would the range of the function y = 600 (3)^x be affected if the function were changed to y = 800 (3)^x ?

a) It changes from y ≥ 600 to y ≥ 800.

b) It would not be affected.

c) It changes from y > 0 to y < 0.

d) It changes from y < 0 to y > 0.

Solution :

Let f(x) = 600 (3)^x and g(x) = 800 (3)^x

To get the function the function g(x) from f(x)

= (4/3) ⋅ 600 (3)^x

Vertical shift and stretch of 4 units and 1/3 units respectively

Considering the vertical asymptotes, for f(x) and g(x) the vertical asymptote is y = 0. 

Problem 7 :

What is the range of the function

y = -10 (1/10)^x

a) y > 0      b)  y < 0       c) y < -10    d)  y > 10

Solution :

From the function, y = -10 (1/10)^x

a = 10, b = 1/10 which is in between 0 and 1.

Since we have negative coefficient, it must have reflection about x-axis along with decay. Horizontal asymptote is y = 0, then its range will be y < 0.

Problem 8 :

What is the domain of the function y = 1500(1.16)^x ?

a)  y > 0      b)  x > 0      c) x ∈ R      d)  0 < x < 1.16

Solution :

y = 1500(1.16)^x

Here a = 1500 and b = 1.16

The value of b is greater than 1, so it must be the exponential growth function. Here we should find domain for the given exponential function, considering all possible inputs, x ∈ R option c is the answer.

Problem 9 :

What is the range of the function

g(x) = 72(0.92)^x ?

a)  y ≥ 72     b)  y > 72      c) y > 0       d) y < 0

Solution :

Here a = 72 and b = 0.92 which lies in between 0 and 1.

It is a decay function and horizontal asymptote is at y = 0.

When x approaches -∞, the output will reach ∞. When x approaches +∞, the output will approach 0. So, the range is y > 0

Problem 10 :

How would the range of the function y = 16(0.75)^x be affected if the function were changed to y = -16(0.75)^x ?

a)  It remains the same.

b)  It changes from y > 16 to y < -16.

c)  It changes from y < 0 to y > 0

d) It changes from y > 0 to y < 0

Solution :

By considering the function y = 16(0.75)^x

a = 16 and b = 0.75 which lies between 0 and 1.

Then it must be a decay function. Finding the graph of the other, their must be a reflection about x-axis since we have negative coefficient.

So, the answer is option d.