GRAPHING EXPONENTIAL DECAY FUNCTIONS

Every exponential function will be in the form y = abx

  • If b > 1, then it must be exponential growth function.
  • If 0 < b < 1, then it must be exponential decay function.

Graphs of exponential growth and decay functions

graphing-exponential-decay-q1

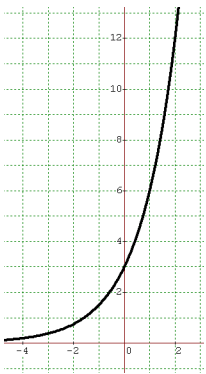
Choosing two points randomly from the graph and applying it, we get

(0, 3) and (2, 12)

y = abx

(0, 3)

3 = ab0

3 = a(1)

a = 3

(2, 12)

12 = 3b2

4 = b2

b = 2

So, the required function will be y = 3(2)x.

Note : Since it is exponential growth function, the value of b is greater than 1

graphing-exponential-decay-q2.png

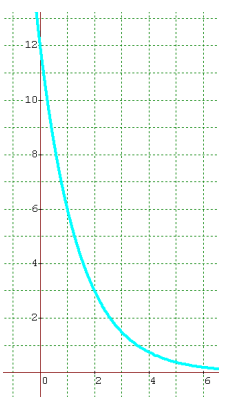
Choosing two points randomly from the graph and applying it, we get

(1, 6) and (2, 3)

y = abx

(1, 6)

6 = ab1

6 = ab-----(1)

(2, 3)

3 = ab2 -----(2)


(2)/(1) ==> ab2 / ab = 3/6 ==> 1/2

b = 1/2

Applying the value of b in (1), we get

6 = a(1/2)

a = 12

Note : Since it is exponential decay function, the value of b is in between 0 and 1.

Sketch the graph of each functions.

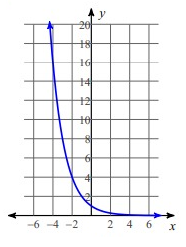
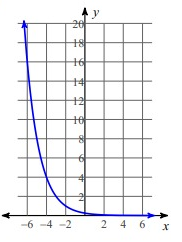
Problem 1 :

y=12x

Solution:

By applying x = -2, then 

y = (1/2)-2

y = 4

If x = -1, then 

y = (1/2)-1

y = 2

If x = 0, then 

y = (1/2)0

y = 1

If x = 1, then 

y = (1/2)1

y = 0.5

If x = 2, then 

y = (1/2)2

y = 0.25

xy-24-120110.520.25
exponential-decay-graph-q1.png

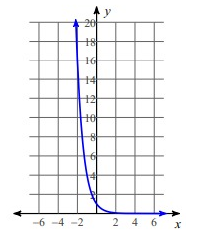
Problem 2 :

y=14x

Solution:

By applying x = -2, then 

y = (1/4)-2

y = 16

If x = -1, then 

y = (1/4)-1

y = 4

If x = 0, then 

y = (1/4)0

y = 1

If x = 1, then 

y = (1/4)1

y = 0.25

If x = 2, then 

y = (1/4)2

y = 0.0625

xy-216-140110.2520.0625
exponential-decay-graph-q2.png

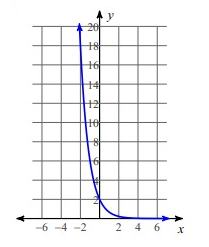
Problem 3 :

y=5⋅12x

Solution:

By applying x = -2, then 

y = 5(1/2)-2

y = 20

If x = -1, then 

y = 5(1/2)-1

y = 10

If x = 0, then 

y = 5(1/2)0

y = 5

If x = 1, then 

y = 5(1/2)1

y = 2.5

If x = 2, then 

y = 5(1/2)2

y = 1.25

xy-220-1100512.521.25
exponential-decay-graph-q3.png

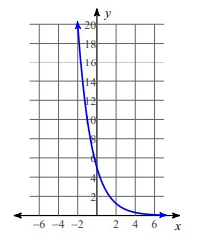
Problem 4 :

y=2⋅12x

Solution:

By applying x = -2, then 

y = 2(1/2)-2

y = 8

If x = -1, then 

y = 2(1/2)-1

y = 4

If x = 0, then 

y = 2(1/2)0

y= 2

If x = 1, then 

y = 2(1/2)1

y= 1

If x = 2, then 

y = 2(1/2)2

y= 0.5

xy-28-14021120.5
exponential-decay-graph-q4.png

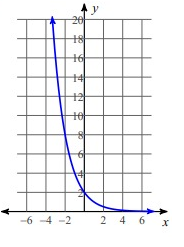
Problem 5 :

y=2⋅13x

Solution:

By applying x = -2, then 

y = 2(1/3)-2

y = 18

If x = -1, then 

y = 2(1/3)-1

y = 6

If x = 0, then 

y = 2(1/3)0

y= 2

If x = 1, then 

y = 2(1/3)1

y = 0.66

If x = 2, then 

y = 2(1/3)2

y = 0.22

xy-218-160210.6620.22
exponential-decay-graph-q5.png

Problem 6 :

y=14⋅12x

Solution:

By applying x = -2, then 

y = 1/4(1/2)-2

y = 1

If x = -1, then 

y = 1/4(1/2)-1

y = 0.5

If x = 0, then 

y = 1/4(1/2)0

y = 0.25

If x = 1, then 

y = 1/4(1/2)1

y = 0.125

If x = 2, then 

y = 1/4(1/2)2

y = 0.0625

xy-21-10.500.2510.12520.0625
exponential-decay-graph-q6.png

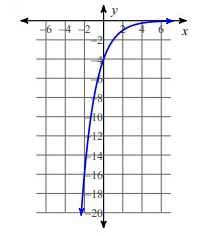
Problem 7 :

y=-2⋅12x

Solution:

By applying x = -2, then 

y = -2(1/2)-2

y = -8

If x = -1, then 

y = -2(1/2)-1

y = -4

If x = 0, then 

y = -2(1/2)0

y = -2

If x = 1, then 

y = -2(1/2)1

y = -1

If x = 2, then 

y = -2(1/2)2

y = -0.5

xy-2-8-1-40-21-12-0.5
exponential-decay-graph-q7.png

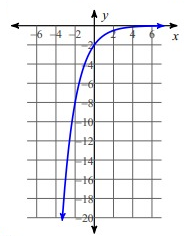
Problem 8 :

y=-4⋅12x

Solution:

By applying x = -2, then 

y = -4(1/2)-2

y = -16

If x = -1, then 

y = -4(1/2)-1

y = -8

If x = 0, then 

y = -4(1/2)0

y = -4

If x = 1, then 

y = -4(1/2)1

y = -2

If x = 2, then 

y = -4(1/2)2

y = -1

xy-2-16-1-80-41-22-1
exponential-decay-graph-q8.png

Recent Articles

RSS

  1. Finding Range of Values Inequality Problems

    May 21, 24 08:51 PM

    Finding Range of Values Inequality Problems

    Read More

  2. Solving Two Step Inequality Word Problems

    May 21, 24 08:51 AM

    Solving Two Step Inequality Word Problems

    Read More

  3. Exponential Function Context and Data Modeling

    May 20, 24 10:45 PM

    Exponential Function Context and Data Modeling

    Read More