GRAPHING ABSOLUTE VALUE FUNCTION

Graph each equation.

Problem 1 :

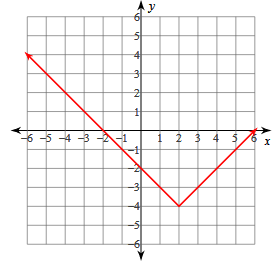
y = |x - 2| - 4

Solution:

Opens upward/Opens downward:

y = a|x - h| + k

y = |x - 2| - 4

a > 0, opens upward

Vertex:

Vertex (h, k) = (2, -4)

x- Intercept: y = 0

0 = |x - 2| - 4

|x - 2| = 4

x - 2 = 4 or x - 2 = -4

x = 6 or x = -2

x- Intercepts = (6, 0) and (-2, 0)

y- Intercept: x = 0

y = |0 - 2| - 4

y = |-2| - 4

y = 2 - 4

y = -2

y- Intercept = (0, -2)

Problem 2 :

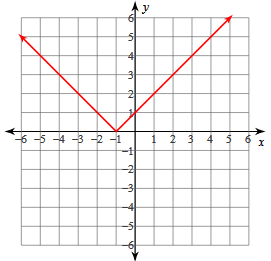
y = |x + 1|

Solution:

Opens upward/Opens downward:

y = a|x - h| + k

y = |x +1|

a > 0, opens upward

Vertex:

Vertex (h, k) = (-1, 0)

x- Intercept: y = 0

0 = |x + 1| 

x + 1 = 0

x = -1

x- Intercept = (-1, 0)

y- Intercept: x = 0

y = |0 + 1| 

y = |1| 

y = 1

y- Intercept = (0, 1)

Problem 3 :

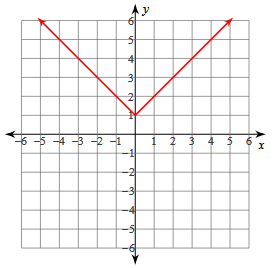
y = |x| + 1

Solution:

Opens upward/Opens downward:

y = a|x - h| + k

y = |x| + 1

a > 0, opens upward

Vertex:

Vertex (h, k) = (0, 1)

x- Intercept: y = 0

0 = |x| + 1

|x| = -1

y- Intercept: x = 0

y = |0| + 1

y = 1

y- Intercept = (0, 1)

Problem 4 :

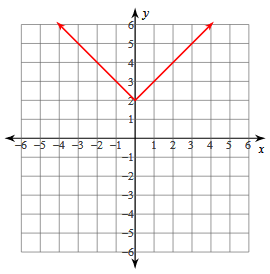
y = |x| + 2

Solution:

Opens upward/Opens downward:

y = a|x - h| + k

y = |x| + 2

a > 0, opens upward

Vertex:

Vertex (h, k) = (0, 2)

x- Intercept: y = 0

0 = |x| + 2

|x| = -2

y- Intercept: x = 0

y = |0| + 2

y = 2

y- Intercept = (0, 2)

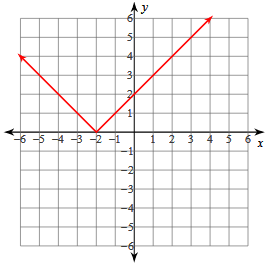
Problem 5 :

y = |x + 2|

Solution:

Opens upward/Opens downward:

y = a|x - h| + k

y = |x + 2| 

a > 0, opens upward

Vertex:

Vertex (h, k) = (-2, 0)

x- Intercept: y = 0

0 = |x + 2| 

x + 2 = 0

x = -2

x- Intercept = (-2, 0)

y- Intercept: x = 0

y = |0 + 2| 

y = 2

y- Intercept = (0, 2)

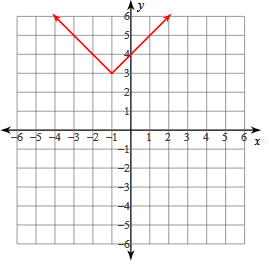
Problem 6 :

y = |x + 1| + 3

Solution:

Opens upward/Opens downward:

y = a|x - h| + k

y = |x + 1| + 3

a > 0, opens upward

Vertex:

Vertex (h, k) = (-1, 3)

x- Intercept: y = 0

0 = |x + 1| + 3

|x + 1| = -3

y- Intercept: x = 0

y = |0 + 1| + 3

y = |1| + 3

y = 1 + 3

y = 4

y- Intercept = (0, 4)

Problem 7 :

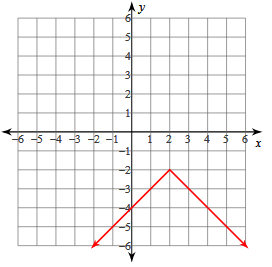
y = - |x - 2| - 2

Solution:

Opens upward/Opens downward:

y = a|x - h| + k

y = -|x - 2| - 2

a < 0, opens downward

Vertex:

Vertex (h, k) = (2, -2)

x- Intercept: y = 0

0 = -|x - 2| - 2

-|x - 2| = 2

y- Intercept: x = 0

y = -|0 - 2| - 2

y = -|-2| - 2

y = -2 - 2

y = -4

y- Intercept = (0, -4)

Problem 8 :

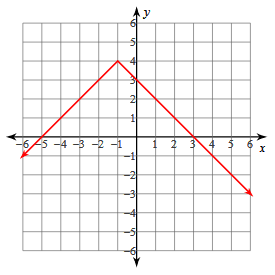
y = - |x + 1| + 4

Solution:

Opens upward/Opens downward:

y = a|x - h| + k

y = -|x + 1| + 4

a < 0, opens downward

Vertex:

Vertex (h, k) = (-1, 4)

x- Intercept: y = 0

0 = -|x + 1| + 4

-|x + 1| = -4

|x + 1| = 4 

x + 1 = 4 or x + 1 = -4

x = 3 or x = -5

x- Intercept = (3, 0) and (-5, 0)

y- Intercept: x = 0

y = -|0 + 1| + 4

y = -|1| + 4

y = -1 + 4

y = 3

y- Intercept = (0, 3)

Problem 9 :

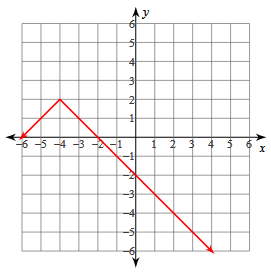
y = -|x + 4| + 2

Solution:

Opens upward/Opens downward:

y = a|x - h| + k

y = -|x + 4| + 2

a < 0, opens downward

Vertex:

Vertex (h, k) = (-4, 2)

x- Intercept: y = 0

0 = -|x + 4| + 2

-|x + 4| = -2

|x + 4| = 2

x + 4 = 2 or x + 4 = -2

x = -2 or x = -6

x- Intercepts = (-2, 0) and (-6, 0)

y- Intercept: x = 0

y = -|0 + 4| + 2

y = -|4| + 2

y = -4 + 2

y = -2

y- Intercept = (0, -2)

Problem 10 :

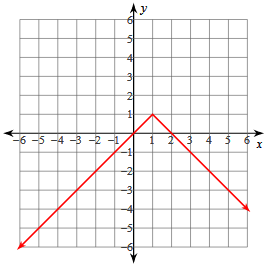
y = -|x - 1| + 1

Solution:

Opens upward/Opens downward:

y = a|x - h| + k

y = -|x - 1| + 1

a < 0, opens downward

Vertex:

Vertex (h, k) = (1, 1)

x- Intercept: y = 0

0 = -|x - 1| + 1

-|x - 1| = -1

|x - 1| = 1

x - 1 = 1 or x - 1 = -1

x = 2 or x = 0

x- Intercepts = (2, 0) and (0, 0)

y- Intercept: x = 0

y = -|0 - 1| + 1

y = -|-1| + 1

y = -1 + 1

y = 0

y- Intercept = (0, 0)

Problem 11 :

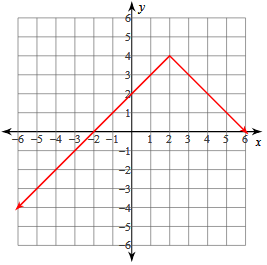
y = - |x - 2| + 4

Solution:

Opens upward/Opens downward:

y = a|x - h| + k

y = -|x - 2| + 4

a < 0, opens downward

Vertex:

Vertex (h, k) = (2, 4)

x- Intercept: y = 0

0 = -|x - 2| + 4

-|x - 2| = -4

|x - 2| = 4

x - 2 = 4 or x - 2 = -4

x = 6 or x = -2

x- Intercepts = (6, 0) and (-2, 0)

y- Intercept: x = 0

y = -|0 - 2| + 4

y = -|-2| + 4

y = -2 + 4

y = 2

y- Intercept = (0, 2)

Problem 12 :

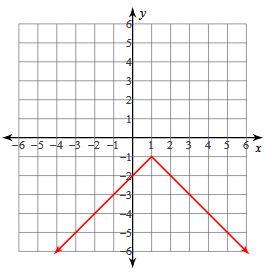
y = -|x - 1| - 1

Solution:

Opens upward/Opens downward:

y = a|x - h| + k

y = -|x - 1| - 1

a < 0, opens downward

Vertex:

Vertex (h, k) = (1, -1)

x- Intercept: y = 0

0 = -|x - 1| - 1

-|x - 1| = 1

y- Intercept: x = 0

y = -|0 - 1| - 1

y = -|-1| - 1

y = -1 - 1

y = -2

y- Intercept = (0, -2)