GRAPH THE ELLIPSE AND IDENTIFY THE CENTER VERTICES AND FOCI
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
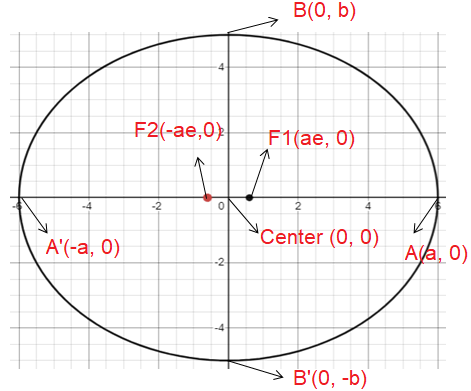
Ellipse Symmetric about x-axis :
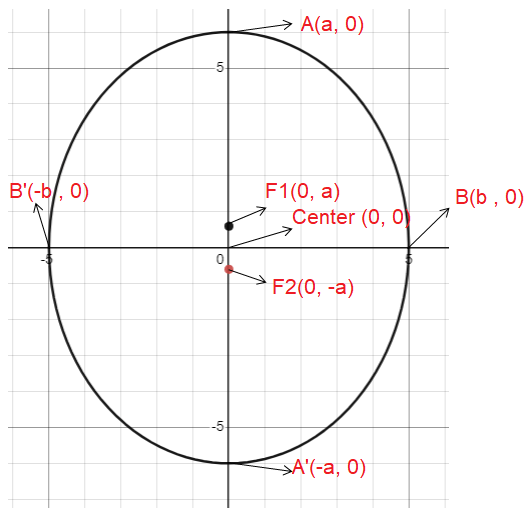
Ellipse Symmetric about y-axis :
Graph the ellipse and identify the center, vertices and foci.
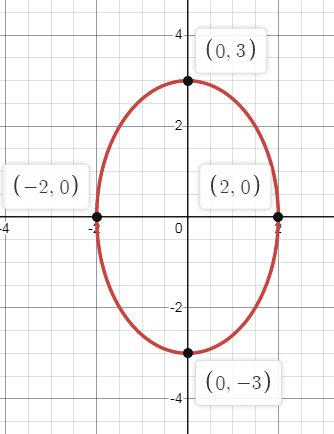
Problem 1 :
Solution:
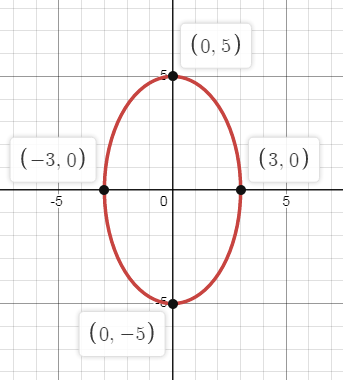
b > a
The above ellipse is symmetric about y-axis.
|
a2 = 25 a2 = 52 a = 5 |
b2 = 9 b2 = 32 b = 3 |
Center:
(0, 0)
Vertices:
A(0, a) and A'(0, -a)
A(0, 5) and A'(0, -5)
Foci:
c2 = a2 - b2
c2 = 52 - 32
= 25 - 9
c2 = 16
c = √16
c = ±4
F1(0, 4) F2(0, -4)
Problem 2 :
4x2 + 9y2 = 36
Solution:
4x2 + 9y2 = 36
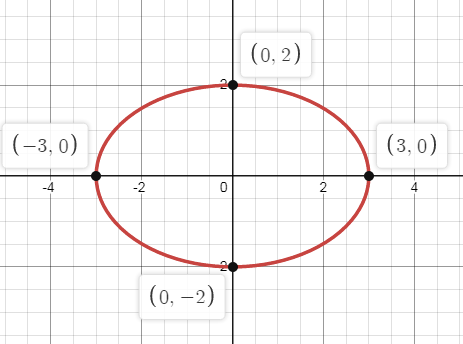
a2 = 9 and b2 = 4
a = 3 and b = 2
Since, a > b, the ellipse symmetric about x-axis.
Center:
(0, 0)
Vertices:
A(a, 0) and A'(-a, 0)
A(3, 0) and A'(-3, 0)
Foci:
c2 = a2 - b2
c2 = 32 - 22
= 9 - 4
c2 = 5
c = ±√5
F1(√5, 0) F2(-√5, 0)
Problem 3 :
x2 + 4y2 = 36
Solution:
x2 + 4y2 = 36
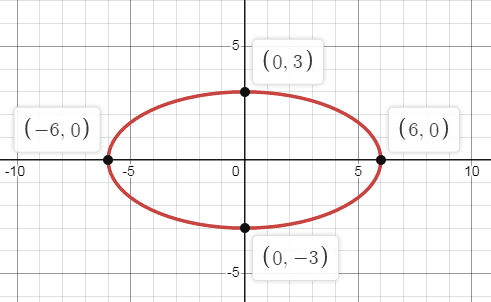
a2 = 36 and b2 = 9
a = 6 and b = 3
Since, a > b, the ellipse symmetric about x-axis.
Center:
(0, 0)
Vertices:
A(a, 0) and A'(-a, 0)
A(6, 0) and A'(-6, 0)
Foci:
c2 = a2 - b2
c2 = 62 - 32
= 36 - 9
c2 = 27
c = ±3√3
F1(3√3, 0) F2(-3√3, 0)
Problem 4 :
Solution:
Let X = x + 1 and Y = y - 3
Since, b > a, the ellipse symmetric about y-axis.
a2 = 4 and b2 = 1
a = 2 and b = 1
Center:
(0, 0)
X = 0 and Y = 0
Substitute X = x + 1 and Y = y - 3
x + 1 = 0 and y - 3 = 0
x = -1 and y = 3
The center is (-1, 3).
Vertices:
A(0, a) and A'(0, -a)
A(0, 2) and A'(0, -2)
|
(0, 2) X = 0 and Y = 2 x + 1 = 0 and y - 3 = 2 x = -1 and y = 5 (-1, 5) |
(0, -2) X = 0 and Y = -2 x + 1 = 0 and y - 3 = -2 x = -1 and y = 1 (-1, 1) |
The vertices are (-1, 5) and (-1, 1).
Foci:
c2 = a2 - b2
= 4 - 1
c2 = 3
c = √3
Here (h, k) = center of the ellipse
h = -1
k = 3
vertical ellipse = (h, k ± c)
= (-1, 3 ± √3)
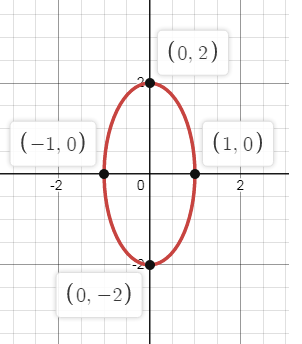
Problem 5 :
Solution:
Let X = x - 1 and Y = y + 2
Since, b > a, the ellipse symmetric about y-axis.
a2 = 9 and b2 = 4
a = 3 and b = 2
Center:
(0, 0)
X = 0 and Y = 0
Substitute X = x - 1 and Y = y + 2
x - 1 = 0 and y + 2 = 0
x = 1 and y = -2
The center is (1, -2).
Vertices:
A(0, a) and A'(0, -a)
A(0, 3) and A'(0, -3)
|
(0, 3) X = 0 and Y = 3 x - 1 = 0 and y + 2 = 3 x = 1 and y = 1 (1, 1) |
(0, -3) X = 0 and Y = -3 x - 1 = 0 and y + 2 = -3 x = 1 and y = -5 (1, -5) |
The vertices are (1, 1) and (1, -5).
Foci:
c2 = a2 - b2
= 9 - 4
c2 = 5
c = √5
Here (h, k) = center of the ellipse
h = 1
k = -2
vertical ellipse = (h, k ± c)
= (1, -2 ± √5)
Problem 6 :
36(x + 4)2 + (y + 3)2 = 36
Solution:
36(x + 4)2 + (y + 3)2 = 36
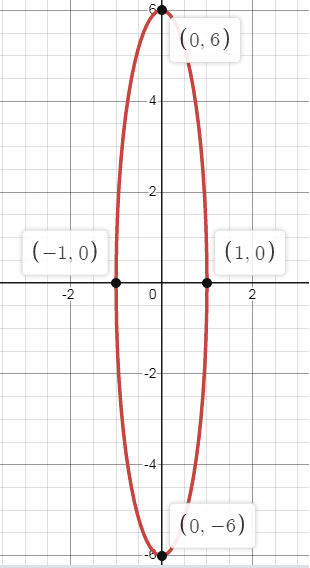
Since, b > a, the ellipse symmetric about y-axis.
a2 = 36 and b2 = 1
a = 6 and b = 1
Center:
(0, 0)
X = 0 and Y = 0
Substitute X = x + 4 and Y = y + 3
x + 4 = 0 and y + 3 = 0
x = -4 and y = -3
The center is (-4, -3).
Vertices:
A(0, a) and A'(0, -a)
A(0, 6) and A'(0, -6)
|
(0, 6) X = 0 and Y = 6 x + 4 = 0 and y + 3 = 6 x = -4 and y = 3 (-4, 3) |
(0, -6) X = 0 and Y = -6 x + 4 = 0 and y + 3 = -6 x = -4 and y = -9 (-4, -9) |
The vertices are (-4, 3) and (-4, -9).
Foci:
c2 = a2 - b2
= 36 - 1
c2 = 35
c = √35
Here (h, k) = center of the ellipse
h = -4
k = -3
vertical ellipse = (h, k ± c)
= (-4, -3 ± √35)
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling