GEOMETRY PROBLEMS USING PROPERTIES OF KITE 

Problem 1 :

Kite Perimeter = _____

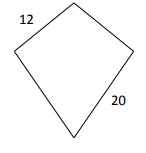
Solution :

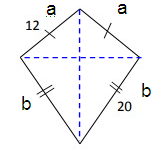
Perimeter of a kite  p = 2(a + b)

a = 12 and b = 20

p = 2(12 + 20)

p = 2(32)

p = 64

So, the perimeter of a kite is 64.

Problem 2 :

Kite x = _____ y = ____ 

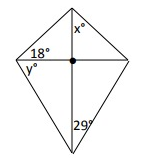
Solution :

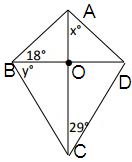
In the above triangle △ABD                                                                   

∠B =18^º and ∠D = 18^º

In the triangle △AOD

∠O = 90^º

∠A = x

sum of interior angle of a triangle = 180^º

∠A + ∠O + ∠D = 180^º

x + 90^º + 18^º = 180^º

x + 108^º = 180^º

x = 180^º - 108^º

x = 72^º

In the triangle △BDC

∠B = ∠D

∠B = y, ∠D = y and ∠C = 29^º

In the triangle △DOC 

∠O = 90^º

Sum of interior angle of a triangle  = 180^º

∠D + ∠O + ∠C = 180^º

y + 90^º + 29^º = 180^º

y + 119^º = 180^º

y = 61^º

So, the values of x and y is 72^º and 61^º.

Problem 3 :

Kite's Perimeter = 86 ft. 

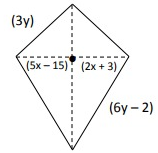
Solution :

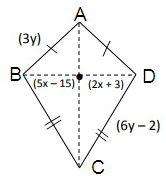
Given, perimeter of a kite = 86 ft.

Perimeter of a kite  p = 2(a + b)

Let a = 3y and b = 6y - 2

86 = 2(3y  + 6y - 2)

86 = 2(9y - 2)

86 = 18y - 4

18y = 86 + 4

18y = 90

y = 90/18

y = 45/9

y = 5

∠B = ∠D

5x - 15 = 2x + 3

5x - 2x = 15 + 3

3x = 18

x = 18/3

x = 6

So, the values of x and y is 6 and 5.

Problem 4 :

Kite

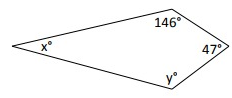
Solution :

By observing the figure,

One pair of opposite angles will be equal.

y = 146^º

The sum of the interior angles of a kite is equal to 360^º.

x + 146^º + 47^º + y = 360^º

x + 146^º + 47^º + 146 = 360^º

x + 339^º = 360^º

x = 360^º - 339^º

x = 21^º

Problem 5 :

Kite

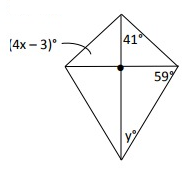
Solution :

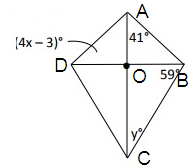
AB = AD

∠ADB = ∠ABD = (4x - 3)^º

∠AOB = 90^º

△ABO :

∠AOB + ∠ABD + ∠OAB = 180^º

90^º + (4x - 3)^º + 41^º = 180^º

131^º + (4x - 3)^º = 180^º

128^º + 4xº = 180^º

4x^º = 180^º - 128^º

4x^º = 52º

x^º = 52º/4

x^º = 13^º

△BEC :

∠BCO + ∠BOC + ∠OBC = 180^º

y^º + 90^º + 59^º = 180^º

y^º + 149^º = 180^º

y^º = 180^º - 149^º

y^º = 31^º

So, the values of x and y is 13^º and 31^º.

Problem 6 :

If WXYZ is a kite, find m ∠XYZ.

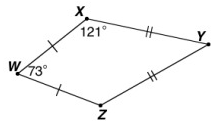
Solution :

By observing the figure,

One pair of opposite angles will be equal.

∠X = 121^º

∠Z = 121^º

The sum of the interior angles of a kite is equal to 360^º.

W + X + Y + Z = 360^º

73^º + 121^º + Y + 121^º = 360^º

315^º + Y= 360^º

Y = 360^º - 315^º

Y = 45^º

Problem 7 :

If MNPQ is a kite, find NP.

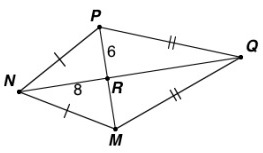
Solution :

Using Pythagorean Theorem :

(NP)² = (NR)² + (PR)²

(NP)² = (8)² + (6)²

(NP)² = 64 + 36

(NP)² = 100

Squaring on both sides.

NP = √100

NP = 10