GEOMETRY PRACTICE QUESTIONS FOR SAT

Problem 1 :

In the figure below, x =

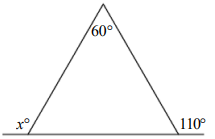
Solution :

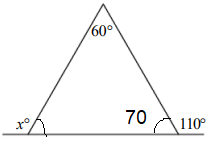
Sum of interior angles of the triangle = 180

60 + 70 + 180 - x = 180

130 + 180 - x = 180

130 + 180 - 180 = x 

x = 130

Problem 2 :

In the figure above, x = 2z and y = 3z . What is the value of z ?

(A) 24        (B) 30        (C) 36         (D) 54           (E) 60

Solution :

Here x and y are supplementary angles.

x + y = 180

2z + 3z = 180

5z = 180

z = 180/5

z = 36

Problem 3 :

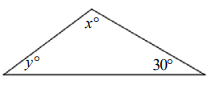
In the figure above, what is in terms of y?

(A) 150 - y  (B) 150 + y   (C) 80 + y   (D) 30 + y   (E) 30 - x

Solution :

Sum of interior angles of the triangle = 180

x + y + 30 = 180

x + y = 180 - 30

x + y = 150

x = 150 - y

Problem 4 :

The angles of a triangle are in the ratio of 2:3:4. What is the degree measure of the largest angle?

Solution :

Interior angles of the triangle is in the ratio 2 : 3 : 4

So, the angles will be 2x , 3x and 4x

2x + 3x + 4x = 180

9x = 180

x = 180/9

x = 20

Largest angle = 4x ==> 4(20)  ==> 80

Problem 5 :

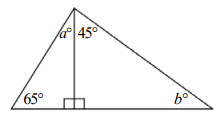
In the figure above, what is the value of a + b?

(A) 45     (B) 70       (C) 90       (D) 145   (E) 170

Solution :

Here angle b should be 45 degree.

The triangle in the left, the sum of interior angles is 180

65 + a + 90 = 180

65 + a = 180 - 90

65 + a = 90

a = 90 - 65

a = 25

a + b = 25 + 45

a + b = 70

Problem 6 :

If two sides of a triangle are 8 and 5, each of the following could be the measure of the third side EXCEPT

(A) 4    (B) 5     (C) 8      (D) 12    (E) 13

Solution :

If a, b and c are sides of the triangle, it should satisfy the triangle inequality theorem.

Let a = 8, b = 5

So, option E is correct.

Problem 7 :

 If the area of a right triangle is 15, what is its perimeter?

(A) 11      (B) 15      (C) 16      (D) 17

(E) The answer cannot be determined from the information provided.

Solution :

To find the perimeter of any right triangle, we should know about all three sides. From the given information, area of right triangle is 15.

1/2 x base x height = 15

base x height = 30

We don't know the hypotenuse, so we cannot find the perimeter of the triangle. So, option E is correct.

Problem 8 :

If the perimeter of isosceles triangle is 20 and the length of side AC is 8, what is one possible value for the length of side BC ?

Solution :

Since it is isosceles triangle, two sides will be equal.

AB = AC = 8, let AB and AC be equal sides. Let x be BC.

Let 8, 8 and x are three sides of the triangle.

Perimeter = 20

8 + 8 + x = 20

16 + x = 20

x = 4

Checking triangle inequality theorem :

8, 8 and 4

8 + 8 > 4

8 + 4 > 8

AB = 8, let AC and BC be equal sides. Let x be BC.

8 + x + x = 20

2x = 20 - 8

2x = 12

x = 6

So, the answers may be 6 or 4.

Problem 9 :

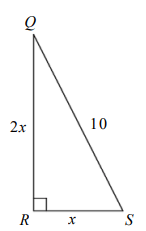
In the figure above, what is the area of right ?

(A) 4 √5     (B) 10     (C) 8 √5     (D) 20    (E) 40

Solution :

Using Pythagorean theorem :

x² + (2x)² = 10²

x² + 4x² = 100

5x² = 100

x² = 20

x = √20

x = 2√5

Area of the triangle = (1/2) x base x height

= (1/2) x 2√5 x 2(2√5)

= √5 x 4√5

= 4(5)

= 20

So, the area of the triangle is 20.

Problem 10 :

In the figure above, if AD || BC, then x = 

(A) 20      (B) 30      (C) 50     (D) 60    (E) 70

Solution :

In triangle DFC,

∠DFC = 180 - (60+70)

∠DFC = 180 - 130

∠DFC = 50

∠BFG = 50

∠FBG = 180 - (50+60)

∠FBG = 180 - 110

∠FBG = 70

x = 70 (corresponding angles)

Problem 11 :

What is the length of the hypotenuse of an isosceles right triangle with an area of 32?

(A) 4    (B) 4√2      (C) 8     (D) 8√2        (E) 3

Solution :

Area of the right triangle = 32

(1/2) x base x height = 32

base x height = 64

Since the given triangle is isosceles right triangle, two sides will be equal. In any right triangle, hypotenuse will be the longest side.

Let base and height of the right triangle be x

x² = 64

x = 8

Using pythagorean theorem,

8² + 8² = (Hypotenuse)²

64 + 64 = (Hypotenuse)²

hypotenuse = √128

= 8√2

Problem 12 :

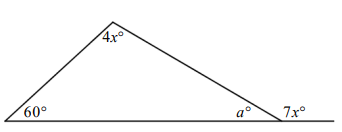
What is the value of a above?

Solution :

a and 7x are linear pairs.

a + 7x = 180 -----(1)

Sum of interior angles of triangle,

4x + 60 + a = 180

4x + a = 180 - 60

4x + a = 120 -----(2)

(1) - (2)

7x - 4x = 180 - 120

3x = 60

x = 60/3

x = 20

Applying the value of x in (2), we get

4(20) + a = 120

80 + a = 120

a = 120 - 80

a = 40

Problem 13 :

In shown above, if QS = 6, RS = 

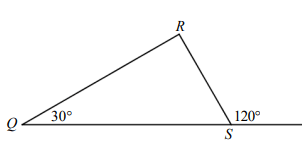
(A) 12     (B) 6√3      (C) 6     (D) 3√3      (E) 3

Solution :

∠RSQ = 180 - 120 ==> 60

In 30-60-90 right triangle,

QS = hypotenuse = 2 (smaller side)

2 RS = 6

RS = 3

Problem 14 :

The length of each side of a certain triangle is an even number. If no two of the sides have the same length, what is the smallest perimeter the triangle could have?

(A) 6     (B) 10      (C) 12      (D) 18     (E) 24

Solution :

Let 2, 4 and 6 are the three measures which are even numbers. To check whether these three measures will create a triangle, we will use triangle inequality theorem.

2 + 4 > 6 (False)

Then these three measures are not sides of the triangle.

4, 6 and 8

4 + 6 > 8 (true)

6 + 8 > 4 (true)

4 + 8 > 6 (true)

So, these three are the measures of the triangle. Finding its perimeter, we get

Perimeter of the triangle = 4 + 6 + 8

= 18

So, option D is correct.