GEOMETRY PRACTICE PROBLEMS FOR SAT

Problem 1 :

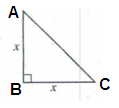
In the figure above, the perimeter of the triangle is 4 + 2√2. What is the value of x?

A) 2      B) 4    C) √2       D) 2√2     E) 2 + √2

Solution:

AC² = AB² + BC²

AC² = x² + x²

AC² = 2x²

AC = √2x

x + x + √2x = 4 + 2√2

2x + √2x = 4 + 2√2

Comparing the corresponding terms, we get

2x = 4

x = 2

So, option (B) is correct.

Problem 2 :

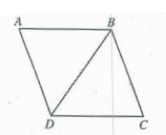
If the five line segments in the figure above are all congruent, what is the ratio of the length of AC (not shown) to the length of BD?

A) √2 to 1     B) √3 to 1     C) √2 to 2

D) √3 to 2        E) √3 to √2

Solution:

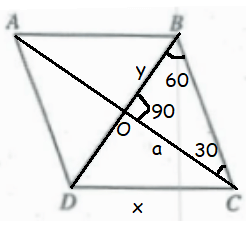
In the picture above, DC = BC = BD. It must be equilateral triangle.

Drawing perpendicular from C to the diagonal, we get 30-60-90 right triangle created by OCB.

sin 60 = opposite side/hypotenuse

√3/2 = a/x

a = x√3/2

cos 60 = adjacent side/hypotenuse

1/2 = y/x

y = x/2

AC : BD = 2a : 2y

= 2(x√3/2) : 2(x/2)

= x√3 : x

= √3 : 1

So, option B is correct.

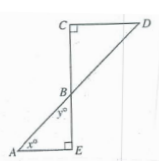
Problem 3 :

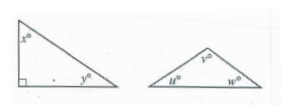
In the triangles above, what is the average (arithmetic mean) of u, v, w, x and y ?

A) 21    B) 45     C) 50      D) 52     E) 54

Solution:

In the above triangle, 

x + y = 90°

u + v + w = 180°

So, option (E) is correct.

Problem 4 :

The perimeter of equilateral triangle ABC is 3 times the perimeter of equilateral triangle DEF. If the perimeter of △DEF is 10, what is the length of one side of △ABC?

A) 3 1/3         B) 10        C) 15     D) 30      E) 40

Solution:

Given, perimeter of △DEF = 10

Perimeter of △ABC = 3 × 10 = 30

So, length of one side of △ABC = 10

So, option (B) is correct.

Problem 5 :

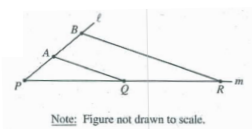
In the figure above, points P, A and B are equally spaced on line l and points P, Q and R are equally spaced on line m. If PB = 4, PR = 6, and AQ = 4, what is the perimeter of quadrilateral QABR?

A) 13        B) 14        C) 15        D) 16      E) 17

Solution:

Perimeter of quadrilateral QABR = 4 + 2 + 6 + 3

= 15

So, option (C) is correct.

Problem 6 :

Solution:

From the picture above, triangles PQT and triangle RPS are similar.

∠QTP = ∠RSP

∠QPT = ∠RPS

So, option (E) is correct.

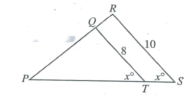
Problem 7 :

In the figure above, AE and CD are each perpendicular to CE. If x = y, the length of AB is 4, and the length of BD is 8, what is the length of CE?

A) 3√2      B) 6√2      C) 8√2     D) 10√2      E) 12√2

Solution :

∠ABE = ∠CBD (vertically opposite angles)

AB = 4, BD = 8

BD is hypotenuse of the triangle BCD

√2 (smaller side) = 8

smaller side = 8/√2

= (8/√2) x (√2/√2)

= 8√2/2

BC = 4√2

AB is the hypotenuse of triangle ABC

√2 (smaller side) = 4

Smaller side = 4/√2

BE = 2√2

CE = BE + BC

=  2√2 +  4√2

=  6√2

So, option B.

Problem 8 :

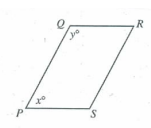
QR || PS in the figure above, what is the value (x + y) ?

A) 90        B) 120    C) 180      D) 270         E) 360

Solution:

Since QR and PS are parallel, co-interior angles add up to 180 degree.

x + y = 180

Problem 9 :

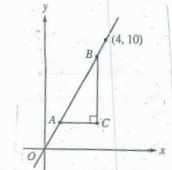
In the figure above, if the legs of triangle ABC are parallel to the axes, which of the following could be the lengths of the sides of triangle ABC?

A) 2, 5, and √29       B) 2, 5, and 7      C) 3, 3 and 3√2

D) 3, 4 and 5       E) 4, 5 and √41

Solution:

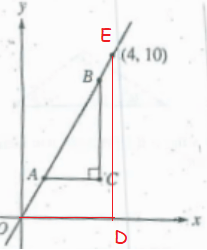
Triangles ODE and ABC are similar.

Since,

∠ACB = ∠ODE

∠BAC = ∠EOD

ED/OD = BC/AC

10/4 = BC/AC

BC = 5 and AC = 2

Hypotenuse = AB

AB² = AC² + BC²

AB² = 2² + 5²

AB² = 4 + 25

AB = √29

So, option A is correct.

Problem 10 :

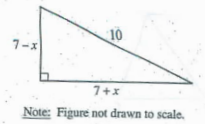
The figure above is a right triangle. What is the value of 49 + x² ?

A) 50         B) 51         C) 72         D) 98       E) 100

Solution:

(7 - x)² + (7 + x)² = 102

49 + x² - 14x + 49 + x² + 14x = 100

98 + 2x² = 100

2(49 + x²) = 100

49 + x² = 100/2

49 + x² = 50

So, option (A) is correct.