GEOMETRY ALGEBRA REVIEW TEST FOR GRADE 8

Problem 1 :

The area of a trapezoid is found using the formula A = 1/2 h(b₁ + b₂), where A is the area, h is the height, and b₁ and b₂ are the lengths of the bases.

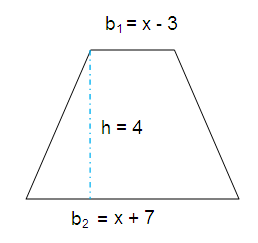
What is the area of the above trapezoid ?

A)  A = 4x + 2               B) A = 4x + 8

C) A = 2x² + 4x - 21      D) A = 2x² + 8x  - 42

Solution :

A = 1/2 h(b₁ + b₂)

height = 4, b₁ = x - 3, b₂ = x + 7

A = ?

A = 1/2 × 4(x - 3 + x + 7)

= 1/2 × 4(2x + 4)

= 2(2x + 4)

A = 4x + 8

Area of the trapezoid is 4x + 8.

So, option B is correct.

Problem 2 :

What is the sum of -3x² - 7x + 9 and -5x² + 6x - 4 ?

Solution :

= -3x² - 7x + 9 + (-5x² + 6x - 4)

= -3x² - 7x + 9 - 5x² + 6x - 4

= -8x² - x + 5

So, option (1) is correct.

Problem 3 :

Which expression is equivalent to (3x⁵ + 17x³ - 1) + (-2x⁵ - 6) ?

A) x⁵ + 17x³ - 7         B) x⁵  - 11x³ - 1

C) 5x³ + 17x³ + 7      D) 6x⁵ + 17x³ + 6

Solution :

= 3x⁵ + 17x³ - 1 + (-2x⁵ - 6)

= 3x⁵ + 17x³ - 1 - 2x⁵ - 6 

= 3x⁵ + 17x³ - 7

So, option A is correct.

Problem 4 :

Find the length of the missing side of the triangle below.

Perimeter = x² + 5x + 11 cm

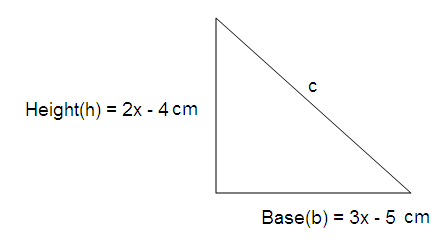
Solution :

P = h + b + c

x² + 5x + 11 = 2x - 4 + 3x - 5 + c

x² + 5x + 11 = 5x - 9 + c

x² + 5x + 11 - 5x + 9 = c

x² + 20 = c

So, the length of the missing side is x² + 20 cm.

Problem 5 :

Approximate the length of the perimeter of the quadrilateral below.

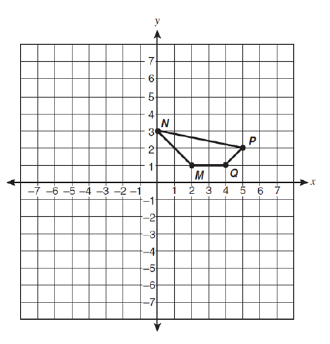
Solution :

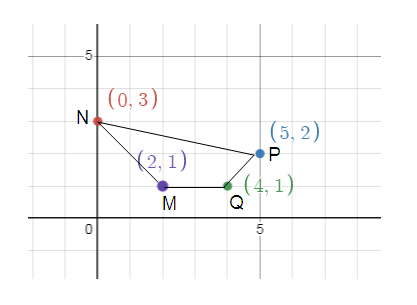
MQ = 2

NM = √[(x₂ - x₁)² + (y₂ - y₁)²]

N = (0, 3) = x₁, y₁

M = (2, 1) = x₂, y₂

NM = √[(2 - 0)² + (1 - 3)²]

= √[(2)² + (-2)²]

= √(4 + 4)

NM = √8

Q = (4, 1) = x₁, y₁

P = (5, 2) = x₂, y₂

QP = √[(5 - 4)² + (2 - 1)²]

= √[(1)² + (1)²]

= √(1 + 1)

QP = √2

N = (0, 3) = x₁, y₁

P = (5, 2) = x₂, y₂

NP = √[(5 - 0)² + (2 - 3)²]

= √[(5)² + (-1)²]

= √(25 + 1)

NP = √26

Perimeter of the quadrilateral = MQ + NM + QP + NP

= 2 + √8 + √2 + √26 

= 2 + 2.8 + 1.4 + 5.1

= 11.3

Problem 6 :

Silvia worked in a store that sold cylinder - shaped children's pools. She made a sign relating the volumes of these two pools.

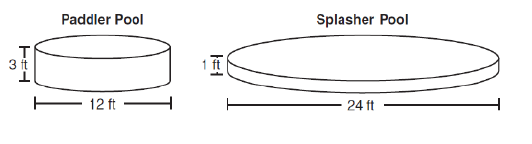
The volume of the Paddler Pool is 108π cubic feet.

The Splasher Pool holds which percent of the water the Paddler Pool holds ?

A. 33%         B 75%          C 133%              D 300%

Solution :

volume of the cylinder = πr²h

Given Paddler Pool = 108 π

Splasher Pool =  π × (12)² × 1

= 144 π

Volume of the Splasher Pool is 144π.

Percent of the water = Splasher Pool/Paddler Pool

= 144 π/108 π

= 1.33

Percent of the water = 1.33 × 100

= 133%

So, option C is correct.

Problem 7 :

A line segment has endpoints J(2, 4) and L(6, 8). The point K is the midpoint of JL What is an equation of a line perpendicular to JL and passing through K ?

A) y = -x + 10           B) y = -x - 10

C) y = x + 2              D) y = x - 2

Solution :

J(2, 4) = (x₁, y₁) 

L(6, 8) = (x₂, y₂)

y = mx + b

6 = -1(4) + b

6 = -4 + b

b = 6 + 4

b = 10

y = -1x + 10

y = -x +10

So, option A is correct.

Problem 8 :

A triangle has vertices at (1, 3), (2, -3), and (-1, -1). What is the approximate perimeter of the triangle ?

A) 10     B 14       C 15           D 16

Solution :

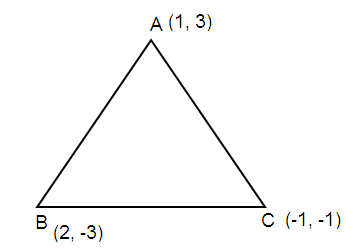
A(1, 3) = (x₁, y₁)

B(2, -3) = (x₂, y₂)

AB = √[(x₂ - x₁)² + (y₂ - y₁)²]

= √[(2 - 1)² + (-3 - 3)²]

= √[(1)² + (-6)²]

= √(1 + 36)

= √37

AB = 6.1

B(2, -3) = (x₁, y₁)

C(-1, -1) = (x₂, y₂)

BC = √[(x₂ - x₁)² + (y₂ - y₁)²]

= √[(-1 - 2)² + (-1 + 3)²]

= √[(-3)² + (2)²]

= √(9 + 4)

= √13

BC = 3.6

A(1, 3) = (x₁, y₁)

C(-1, -1) = (x₂, y₂)

CA = √[(x₂ - x₁)² + (y₂ - y₁)²]

= √[(-1 - 1)² + (-1 - 3)²]

= √[(-2)² + (-4)²]

= √(4 + 16)

= √20

AC = 4.5

Perimeter = AB + BC + CA

= 6.1 + 3.6 + 4.5

= 14.2

So, perimeter of the triangle is 14.2.

So, option B is correct.

Problem 9 :

The vertices of quadrilateral EFGH are E(-7, 3), F(-4, 6), G(5, -3), and H(2, -6), What kind of quadrilateral is EFGH ? 

A) trapezoid       B) square   C) rectangle that is not a square     D) rhombus that is not a square

Solution :

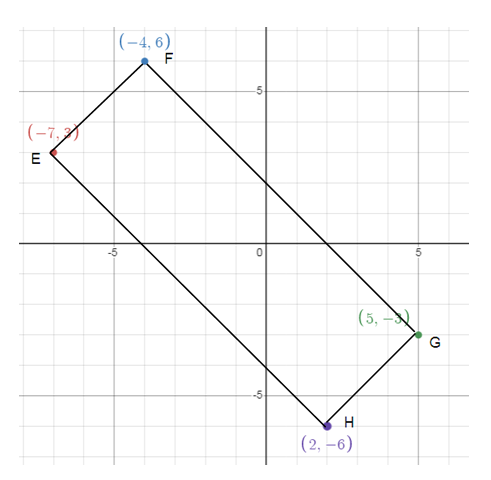
So, option C is correct.

Problem 10 :

R is the midpoint of segment PS, Q is the midpoint of segment RS.

P is located at (8, 10),and S is located at (12, -6). What are the coordinates of Q ?

A) (4, 2)         B (2, -8)        C (11, -2)            D (10, 2)

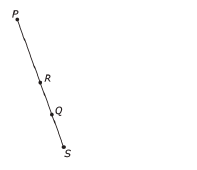
Solution :

P is located at (8, 10) = x₁, y₁

S is located at (12, -6) = x₂, y₂

So, the coordinates of Q is (11, -2).

So, option C is correct.

Problem 11 :

County X has a population density of 250 people per square mile. The total population of the county is 150,000. Which geometric model could be the shape of county X?

A)  a parallelogram with a base of 25 miles and a height of 25 miles.

B) a rectangle that is 15 miles long and 45 miles wide

C) a right triangle with a leg that is 30 miles long and a hypotenuse that is 50 miles long 

D) a trapezoid with base lengths of 10 miles and 30 miles and a height of 25 miles.

Solution :

Population density = 250

Total population of the county = 150,000

Total area which represents the population = Total population/Population density

= 150000/250

= 600 square miles

A) area of parallelogram = Base × Height

= 25 × 25

= 625 square miles.

Which is not equal to 600 square miles.

So it's not the correct option.

B) area of a rectangle = Length × Width

= 15 × 45

= 675 square miles

675 square miles not equal to 600 square miles.

So it's not the correct option.

C) area of a right triangle = Base × Height

Since length of hypotenuse is given.

So we will find the length of height.

Height = √[Hypotenuse)² - (Base)²]

= √(50)² - (30)²

= √1600

Height = 40 miles

So, area of the  right triangle= 1/2 (Base × Height)

= 1/2 (40 × 30)

= 1/2 (1200)

= 600 square miles

Which matches the area of country x.

So, it's correct option.

Problem 12 :

A company is designing a cylinder to hold marbles for a new game it is inventing. The cylinder has a height of 18 inches and a diameter of 6 inches. Find the volume of the cylinder to the nearest of a cubic inch.

[1] 108.0      [2] 508.9      [3] 678.6     [4] 1065.92

Solution :

height = 18 inches

diameter = 6 inches

v = πr²h

d = 2r

6 = 2r

6/2 = r

3 = r

v = 3.14 × (3)² × 18

= 3.14 × 9 × 18

v = 508.68

So, option [2] is correct.