GEOMETRIC MEAN THEOREM
Proof of Geometric Mean Theorem :
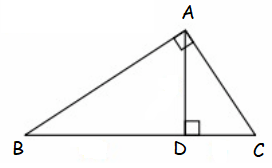
The length of the altitude drawn from the right angle of a triangle to its hypotenuse is equal to the geometric mean of the lengths of the segments formed on the hypotenuse.
AD = √(BD ⋅ DC)
Proof :
Triangles ABC, ADC and ABD are right triangles. Here
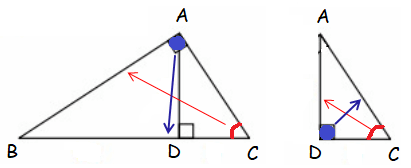
Triangle ABC Triangle ADC
∠BAC = ∠ADC
∠ACB = ∠ACD
Triangle ABC ~ triangle ADC
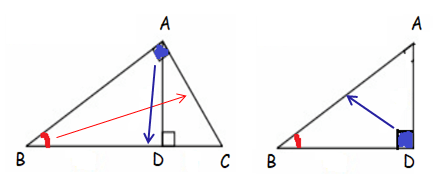
Triangle ABC Triangle ABD
∠BAC = ∠ADB
∠ABC = ∠ABD
Triangle ABC ~ triangle ADB
Solve for the missing variable.
Problem 1 :
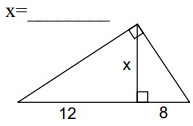
Solution:
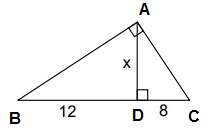
ABC is a right triangle and AD is the altitude drawn from the right angle A.
So, AD is the geometric mean between BD and DC.
AD = √(BD ⋅ DC)
x = √(12 ⋅ 8)
x = √96
x = 9.79
Problem 2 :
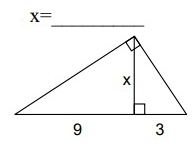
Solution:
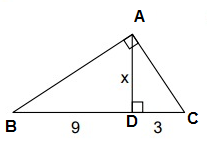
ABC is a right triangle and AD is the altitude drawn from the right angle A.
So, AD is the geometric mean between BD and DC.
AD = √(BD ⋅ DC)
x = √(9 ⋅ 3)
x = √27
x = 3√3
Problem 3 :
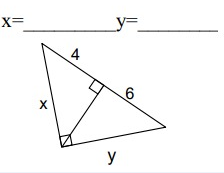
Solution:
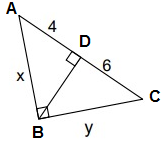
AC = AD + DC
AC = 4 + 6
AC = 10
ABC is a right triangle and BD is the altitude drawn from the right angle B.
So, BA is the geometric mean between AD and AC.
BA = √(AD ⋅ AC)
x = √(4 ⋅ 10)
x = √40
x = 6.32
So, BC is the geometric mean between CD and AC.
BC = √(CD ⋅ AC)
y = √(6 ⋅ 10)
y = √60
y = 7.74
Problem 4 :
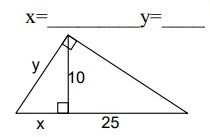
Solution:
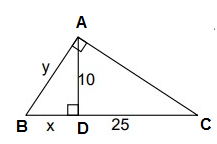
ABC is a right triangle and AD is the altitude drawn from the right angle A.
So, AD is the geometric mean between BD and DC.
AD = √(BD ⋅ DC)
10 = √(x ⋅ 25)
102 = 25x
100 = 25x
x = 4
In right triangle ABD,
y2 = x2 + 102
y2 = 42 + 102
y2 = 16 + 100
y2 = 116
y = √116
y = 10.77
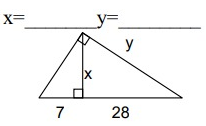
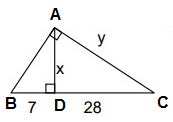
Problem 5 :
Solution:
ABC is a right triangle and AD is the altitude drawn from the right angle A.
So, AD is the geometric mean between BD and DC.
AD = √(BD ⋅ DC)
x = √(7 ⋅ 28)
x = √196
x = 14
In right triangle ABD,
y2 = x2 + 72
y2 = 142 + 72
y2 = 196 + 49
y2 = 245
y = √245
y = 15.65
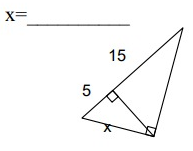
Problem 6 :
Solution:
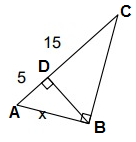
AC = AD + DC
AC = 5 + 15
AC = 20
ABC is a right triangle and BD is the altitude drawn from the right angle B.
So, AB is the geometric mean between AD and AC.
AB = √(AD ⋅ AC)
x = √(5 ⋅ 20)
x = √100
x = 10
Problem 7 :
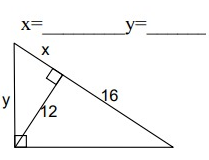
Solution:
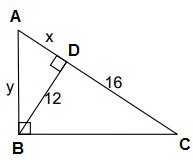
ABC is a right triangle and BD is the altitude drawn from the right angle B.
So, BD is the geometric mean between AD and DC.
BD = √(AD ⋅ DC)
12 = √(x ⋅ 16)
122 = 16x
144 = 16x
x = 9
In right triangle ABD,
y2 = x2 + 122
y2 = 92 + 122
y2 = 81 + 144
y2 = 225
y = √225
y = 15
Problem 8 :
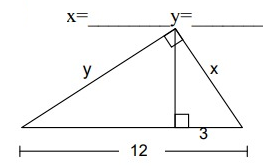
Solution:
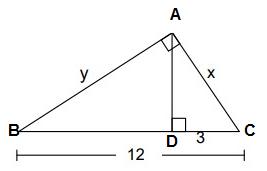
BC = BD + DC
12 = BD + 3
BD = 9
ABC is a right triangle and AD is the altitude drawn from the right angle A.
AC is the geometric mean between DC and BC.
AC = √(DC ⋅ BC)
x = √(3 ⋅ 12)
x = √36
x = 6
AB is the geometric mean between BD and BC.
AB = √(BD ⋅ BC)
y = √(9 ⋅ 12)
y = √108
x = 10.39
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling