FUNCTION OPERATIONS WITH SET OF ORDERED PAIRS

Problem 1 :

Given the function

𝑓 = {(−3, 4), (−2, 2), (−1, 0), (0, 1), (1, 3), (2, 4), (3, −1)}

and the function

𝑔 = {(−3, −2), (−2,0), (−1, −4), (0,0), (1, −3), (2, 1), (3, 2)}

compute the following values. 

Solution :

a) (f + g)(-3)

= f(-3) + g(-3)

= 4 + (-2)

(f + g)(-3) = 2

b)  (f - g) (2)

= f(2) - g(2)

= 4 - 1

(f - g) (2) = 3

c)  (fg)(-1)

= f(-1) g(-1)

= 0(-4)

(fg)(-1) = 0

d)  (g - f)(3)

= g(3) - f(3)

= -1 - 2

(g - f)(3) = -3

e)  (f/g)(-2) 

= f(-2) / g(-2)

=  2/0

(f/g)(-2) = undefined

f)  (g/f)(3)

= g(3) / f(3)

= 2/(-1)

(g/f)(3) = -2

Problem 2 :

Use the graph to determine each of the following. Assume integer answers. The graph of g is the graph in bold.

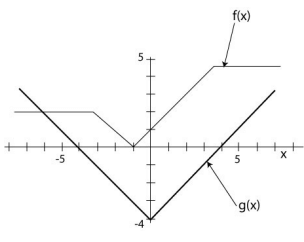
Complete the following ordered pairs from the graphs above. Use the information to help you with the problems below. The first ordered pair for each function has been completed for you.

f: (–7, 2), (–6,  ), (–5,  ), (–4,  ), (–3, ), (–2, ), (–1, ), (0,  ), (1, ), (2, ), (3, ), (4, ), (5, ), (6, ), (7, )

g: (–7, 3), (–6, ), (–5, ), (–4, ), (–3, ), (–2, ), (–1, ), (0, ), (1, ), (2, ), (3, ), (4, ), (5, ), (6, ), (7, )

Solution :

By observing the given graph, we get the ordered pairs,

f: (–7, 2), (–6, 2), (–5, 1), (–4, 0), (–3, 2), (–2, 1), (–1, 0), (0, 1 ), (1, 2), (2, 3), (3, 4), (4, 5), (5, 5), (6, 5), (7, 5)

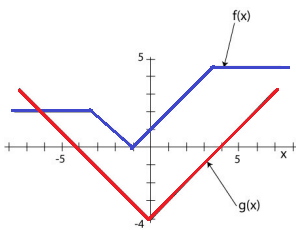
g: (–7, 3), (–6, 2), (–5, 1), (–4, 0), (–3, -1), (–2, -2), (–1, -3), (0, -4), (1, -3), (2, -2), (3, -1), (4, 0), (5, 1), (6, 2), (7, 3)

a) g(4) = 0

b) f(2) = 3

c) g(0) = -4

d) f(-6) = 2

e) If f (x) = 0, x =

Here output is 0, when x = ?

x = -1

f) If g(x) = 0, x =

For -4 and 4, we get 0 as output.

Problem 3 :

For

f = {(1, 2), (3, 3), (2, 4), (4, 1)}

and

g = {(1, 3), (3, 4), (2, 2), (4, 1)}

find f ◦ g and g ◦ f if they exist.

Solution :

Evaluating (f ◦ g) (x) :

Let us calculate (f ◦ g) (1), (f ◦ g) (2), (f ◦ g) (3) and (f ◦ g) (4)

(f ◦ g) (x) = {(1, 3) (2, 4) (3, 1) (4, 2)}

Then (f ◦ g) (x) exists.

Evaluating (g ◦ f) (x) :

Let us calculate (g ◦ f) (1), (g ◦ f) (2), (g ◦ f) (3) and (g ◦ f) (4)

(g ◦ f) (x) = {(1, 2) (2, 1) (3, 4) (4, 3)}

Then (f ◦ g) (x) exists.

Problem 4 :

Lisa makes $18 per hour at her new part-time job.

a) Write a function, I, to represent Lisa’s income for the week if she works h hours. Complete the table below.

I(h) =

b) Lisa puts 10% of her salary in her bank savings every week and $10 into her piggy bank for a rainy day. Write a function, S, to represent the total amount of money she saves each week if her income is I dollars. Complete the table below.

S(I) =

c) Using the information above, write a formula for S(I(h)) and complete the table below.

S(I(h)) =

Solution :

a)  Here h is the number of hours she is working

I(h) = 18h

b) S(I) = 0.10h + 10

c)  S(I(h)) =

S(I) = 0.10h + 10 and I(h) = 18h

S(I(h)) = S(18h)

= 0.10 (18h) + 10

= 1.8h + 10