FUNCTION NOTATION SAT PROBLEMS

Problem 1 :

In the table above, if y = x² + x - 2, what is the value of k ?

Solution :

So, the value of k is 18.

Problem 2 :

The function f is defined by f(x) = x²+bx+c where b and c are constants. If the graph of f has x-intercepts at -5 and 3, which of the following correctly gives the values of b and c ?

a)  b = -5, c = 3           b) b = -3, c = 5

 c)  b = -2, c = -15        d)  b = 2, c = -15

Solution :

x-intercepts are at -5 and 3.

When x = -5, y = 0

f(-5) = (-5)²+b(-5)+c

0 = 25 - 5b + c

-5b + c = -25

5b - c = 25 ------(1)

When x = 3, y = 0

f(3) = 3²+b(3)+c

0 = 9 + 3b + c

3b + c = -9 ------(2)

(1) + (2)

8b = 25 - 9

8b = 16

b = 2

Applying the value of b in (1), we get

5(2) - c = 25

10 - 25 = c

c = -15

Problem 3 :

The distance d in meter traveled by a rocket depends on the amount of fuel f in liters, it burns according to the equation

d = 2f/3

Based on the table above, how many rockets traveled more than 20 meters ?

a)  One           b) Two     c) Three        d)  Four

Solution :

When f = 32,  d > 20

When f = 35, d > 20

So, two rockets travelled more than 20 meters.

Problem 4 :

g(x) = √(x - 1)(x- 2)

What is one possible value of x for which the function g above is undefined ?

Solution :

If x = 1 or x = 2, then g(x) will become 0. It is defined only.

If 1 < x < 2, then g(x) < 0, then the function will become undefined.

Problem 5 :

Let the function f be defined by f(x) = 2x³ - 1 and let the function g be defined by g(x) = x² + 3, what is the value of f(g(1)) ?

a)  4      b)  23     c)  56    d)  127

Solution : 

g(x) = x² + 3

g(1) = 1² + 3

g(1) = 4

f(g(1)) = f(4)

f(4) = 2(4)³ - 1

f(4) = 2(64) - 1

f(4) = 128 - 1 ==> 127

Problem 6 :

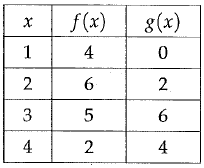
Four values for the functions f and g are shown in the table above. If g(m) = 6, what is the value of f(m) ?

Solution :

From the table, for what of x we get 6 in the column g(x).

g(3) = 6

Comparing g(3) = 6 and g(m) = 6, m = 3

Find f(m), that is f(3) = 5.

So, the answer is 5.

Problem 7 :

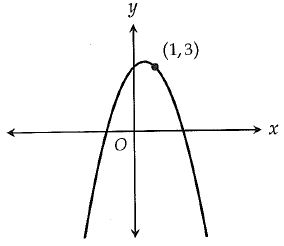
The graph of the function g in the xy plane is shown above. If f is another function defined in the same xy-plane and f(1) = 1, then g could be which of the following ?

a)  f - 1      b)  f - 2     c) f + 1      d) f + 2

Solution :

The given function is g.

g(1) = 3

Given that f(1) = 1

So, f + 2 is correct.

Problem 8 :

f(x) = ax³ + b

In the function f defined above, a and b are constants. If f(-1) = 4 and f(1) = 10, what is the value of b ?

Solution :

f(-1) = 4 and f(1) = 10

f(x) = ax³ + b

f(-1) = a(-1)³ + b

4 = -a + b ---------(1)

f(1) = a(1)³ + b

10 = a + b ---------(2)

(1) + (2)

2b = 14

b = 7

Applying the value of b in (1), we get

-a + 7 = 4

-a = 4 - 7

a = 3

Problem 9 :

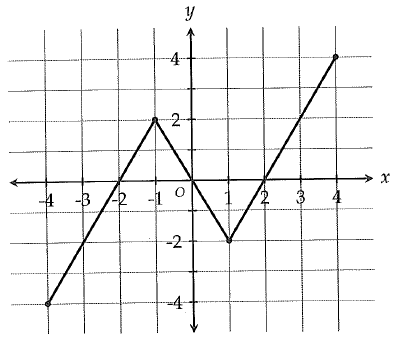
The function f is graphed in the xy plane above. If f(c) = f(3), which of the following could be the value of c ?

a)  -3       b)  -2       c) -1         d)  2

Solution :

Given, f(c) = f(3)

f(3) = 2

So, f(c) = 2

From the graph, f(-1) = 2. So, the value of c is -1.

Problem 10 :

For all x ≥ 3,

f(x) = √(x - 3)/2. If f(n) = 3

what is the value of n ? 

Solution :

f(x) = √(x - 3)/2

f(n) = √(n - 3)/2

3 = √(n - 3)/2

6 = √(n - 3)

36 = n - 3

n = 39

So, the value of n is 39.

Problem 11 :

The function f is defined by f(x) = 2x² - ax - 7, where a is constant. If the graph of f intersects the x-axis at (-1, 0), what is the value of a ?

a)  -9       b)  -5        c)  5         d)  9

Solution :

f(x) = 2x² - ax - 7

The graph f intersects the x-axis at (-1, 0).

When x = -1, y = 0

f(-1) = 2(-1)² - a(-1) - 7

0 = 2 + a  - 7

0 = -5 + a

a = 5

Problem 12 :

If f(4) = -2, which of the following cannot be the definition of f ?

a)  f(x) = x - 6       b)  f(x) = x² - 4x - 2

c) f(x) = -3x + 14         d)  f(x) = -2(x - 3)²

Solution :