FROM THE SHADED REGION FIND THE INEQULAITY

For each region below,

i) Find the equation of the line which forms the boundary and

ii) Find the inequality represented by the region.

Problem 1 :

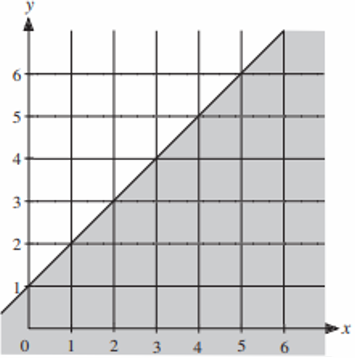
Solution :

The given is solid line. So, when we represent it as inequality, we have to use any one of the signs ≤ or ≥.

i)  Slope = rise/run = 1

y-intercept = 1

So, equation of the boundary will be y = 1x + 1

ii) Selecting one of the point from the shaded region, say (2, 2) and applying in the equation above, we get

2 ___ 2 + 1

2 ___ 3

To make it as true, we have to use the sign ≤. So, the required inequality represented by the shaded region will be

y ≤ 1x + 1

Problem 2 :

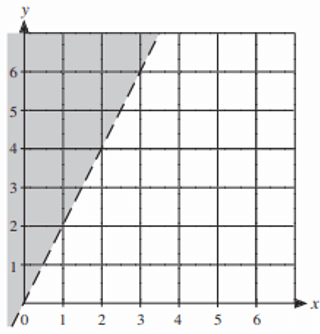
Solution :

The given is dotted line. So, when we represent it as inequality, we have to use any one of the signs < or >.

i)  Slope = rise/run = 2/1

y-intercept = 0

So, equation of the boundary will be y = 2x + 0

ii) Selecting one of the point from the shaded region, say (2, 3) and applying in the equation above, we get

3 ___ 2(1)

3 __ 2

To make it as true, we have to use the sign >. So, the required inequality represented by the shaded region will be

y > 2x

Problem 3 :

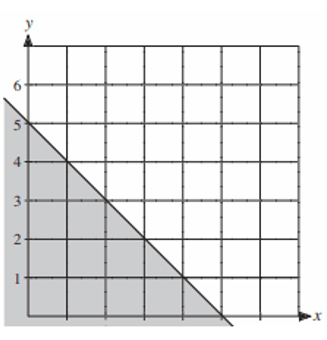
Solution :

The given is solid line. So, when we represent it as inequality, we have to use any one of the signs ≤ or ≥.

i)  Slope = rise/run = -1/1

y-intercept = 5

So, equation of the boundary will be y = -1x + 5

ii) Selecting one of the point from the shaded region, say (1, 3) and applying in the equation above, we get

3 ___ -1 + 5

3 ___ 4

To make it as true, we have to use the sign ≤. So, the required inequality represented by the shaded region will be

y ≤ -1x + 5

Problem 4 :

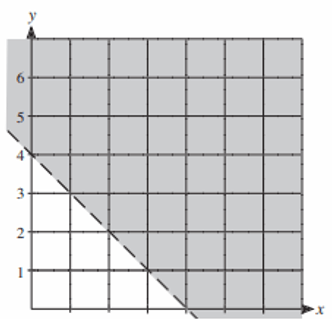
Solution :

The given is dotted line. So, when we represent it as inequality, we have to use any one of the signs < or >.

i)  Slope = rise/run = -1/1

y-intercept = 4

So, equation of the boundary will be y = -1x + 4

ii) Selecting one of the point from the shaded region, say (3, 2) and applying in the equation above, we get

2 ___ -1(3) + 4

2 ___ -3 + 4

2 ___ 1

To make it as true, we have to use the sign ≤. So, the required inequality represented by the shaded region will be

y ≥ -1x + 4

Problem 5 :

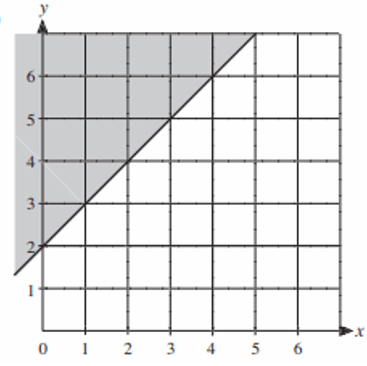
Solution :

The given is solid line. So, when we represent it as inequality, we have to use any one of the signs ≤ or ≥.

i)  Slope = rise/run = 1/1

y-intercept = 2

So, equation of the boundary will be y = x + 2

ii) Selecting one of the point from the shaded region, say (1, 4) and applying in the equation above, we get

4 ___ 1 + 2

4 ___ 3

To make it as true, we have to use the sign ≥. So, the required inequality represented by the shaded region will be

y ≥ x + 2

Problem 6 :

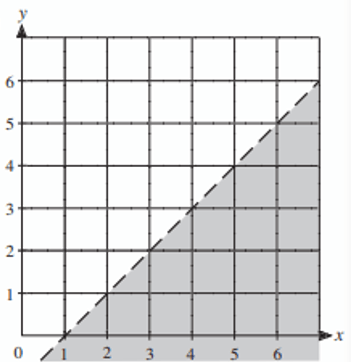
Solution :

The given is solid line. So, when we represent it as inequality, we have to use any one of the signs < or >.

i)  Slope = rise/run = 1/1

Since we don't see y-intercept, we have to use point slope form to find equation of the line.

(2, 1) is one of the point of the line.

(y - y₁) = m (x - x₁)

(y - 1) = 1(x - 2)

y - 1 = x - 2

y = x - 2 + 1

y = x - 1

Selecting one of the points from the shades region say (4, 2).

2 ___ 4 - 1

2 ___ 3

To make it as true, we have to use the sign <. So, the required inequality

y < x - 1