FROM THE NET DIAGRAM OF CUBE AND CUBOID FIND SURFACE AREA AND VOLUME

Cuboid

The net of a cuboid is made up of 6 rectangles. The rectangles will occur in pairs as illustrated below

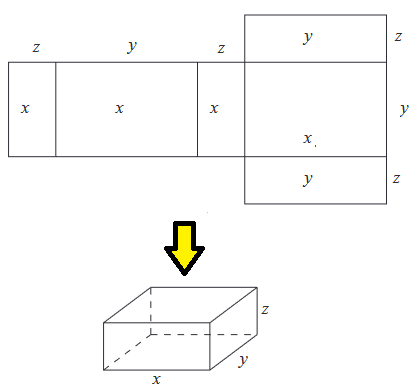
Cube

A solid shape whose faces are only squares is called a “cube”

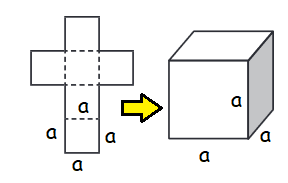
Work out the surface area of these cubes :

Problem 1 :

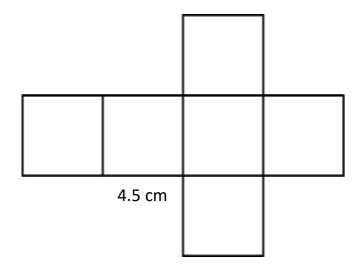
Solution :

Surface Area of a Cube = 6a²

= 6 × 4.5 × 4.5

= 121.5 cm²

Volume of a Cube = a³

= 4.5 × 4.5 × 4.5

= 91.125 cm³

Problem 2 :

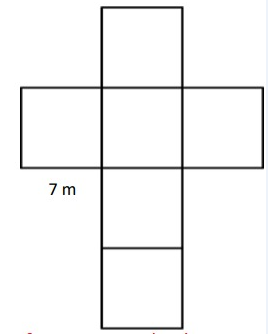
Solution :

Surface Area of a Cube = 6a²

= 6 × 7 × 7

= 294 m²

Volume of a Cube = a³

= 7 × 7 × 7

= 343 m³

Find the surface area of each of these cuboids :

Problem 3 :

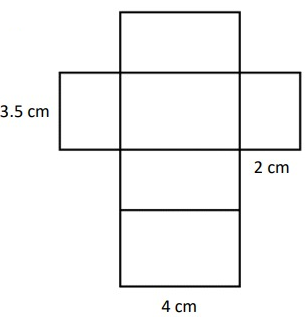
Solution :

Surface Area of a Cuboid = 2(lw + wh + lh)

length = 4 cm

width = 2 cm

height = 3.5 cm

= 2(4 × 2 + 2 × 3.5 + 4 × 3.5)

= 2(8 + 7 + 14)

= 2(29)

= 58 cm²

Volume of a Cube = l × w × h

= 4 × 2 × 3.5

= 28 cm³

Problem 4 :

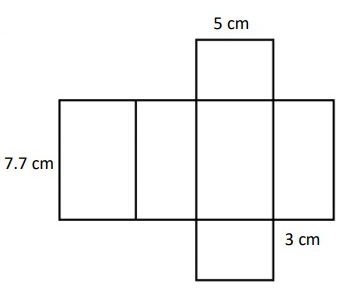
Solution :

Surface Area of a Cuboid = 2(lw + wh + lh)

length = 5 cm

width = 3 cm

height = 7.7 cm

= 2(5 × 3 + 3 × 7.7 + 5 × 7.7)

= 2(15 + 23.1 + 38.5)

= 2(76.6)

= 153.2 cm²

Volume of a Cube = l × w × h

= 5 × 3 × 7.7

= 115.5 cm³

Problem 5 :

The volume of a cube is 729 cm³. Find the length of the cube.

Solution :

Given, the volume of a cube is 729cm³

To find, the length of the cube.

The volume of the cube = a³

a³ = 729cm³

a = ∛729

a = 9

∴ the length of the cube.= 9cm.

Problem 6 :

The area of one face of a cube is 36 cm². Find

(a)  The length of the cube

(b)  The total surface area of the cube

(c)  The volume of the cube

Solution :

Area of one face of a cube is 36 cm².

(a) Let x be the length of the cube.

v = x³ 

36 = x³

Taking cube root on each sides.

∛36 = ∛x³

x = ∛36

So, the length of the cube is ∛36 cm.

(b)  The total surface area of the cube = 6a²

6a² = 36

a² = 36/6

a² = 6

Taking square root on each sides.

√a² = √6

a = √6

(c)  The volume of the cube = a³

= √6 × √6 × √6

= 6√6

= 6 × 2.45

= 14.7

So, volume of the cube is 14.7 cm³.

Problem 7 :

The total surface area of a cube is 294 cm². Find :

(a)  The area of one face of the cube

(b)  The length of the cube

(c)  The volume of the cube

Solution :

Total surface area of a cube is 294 cm².

(a) The total surface area of the cube = 6a²

6a² = 294

a² = 294/6

a² = 49

a = 7 cm

So, area of one face of the cube is 7cm.

(b) Let x be the length of the cube.

v = x³ 

294 = x³

Taking cube root on each sides.

∛294 = ∛x³

x = ∛294

(c)  The volume of the cube = a³

= 7 × 7 × 7

= 343

So, volume of the cube is 343 cm³.

Problem 8 :

The surface area of this cuboid is 102 cm².What is the length marked x ?

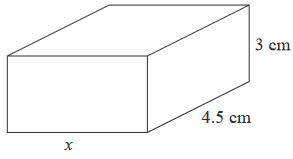
Solution :

surface area of this cuboid = 102 cm²

Length = 4.5 cm, width = x and height = 3 cm

2(lw + wh + hl) = 102

2(4.5x + 3x + 3(4.5)) = 102

2(4.5x + 3x + 13.5) = 102

7.5x + 13.5 = 51

7.5x = 51 - 13.5

7.5x = 37.5

x = 37.5/7.5

x = 5

So, width of the cuboid is 5 cm.