FROM THE GRAPH OF THE FUNCTION FIND THE GRAPH OF ITS DERIVATIVE

How to match the graph of function f(x) to its derivative graph ?

The following points to be noted from the graph of original function.

• If the given function f(x) is increasing on the interval, then its derivative function will have positive slope and that should be above the x-axis.
• If the given function f(x) is decreasing on the interval, then its derivative function will have negative slope and that should be below the x-axis.
• The values that we are deriving by equating the first derivative to 0, that is f'(x) = 0 are critical numbers. These critical numbers are x-intercepts in the derivative graph.

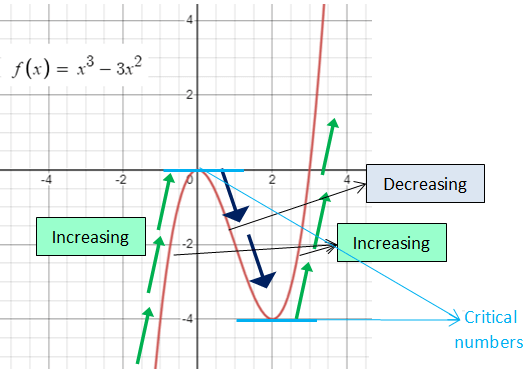
From graph of f(x) (-∞, 0) --> Increasing (0, 2) --> Decreasing (2, ∞) --> Increasing At x = 0 and x = 2, there are critical numbers

From graph of f'(x) (-∞, 0) --> above the x-axis (0, 2) --> below the x-axis (2, ∞) --> above the x-axis At x = 0 and x = 2, there are x-intercepts

The graph of a function is given. Choose the answer that represents the graph of its derivative.

Problem 1 :

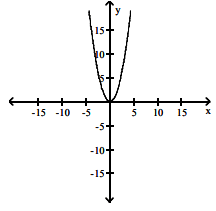
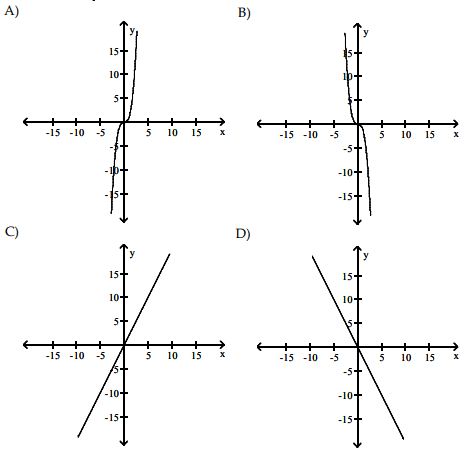
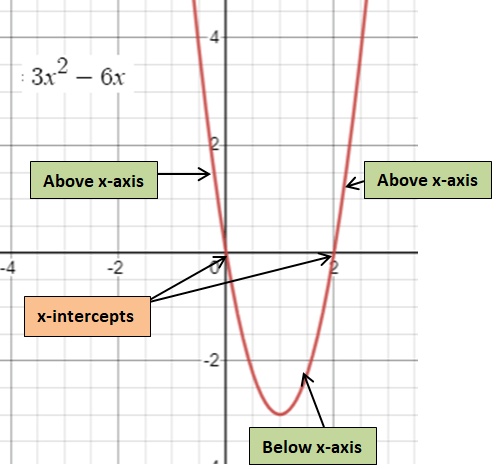
Solution :

In the question, the given curve is a parabola which will have the highest exponent of 2. So, its derivative will have the highest exponent of 1. Then it must be a straight line.

• On the interval (-∞, 0), the function is decreasing.
• On the interval (0, ∞), the function is increasing.

In the derivative graph the curve should be below the x-axis in the interval (-∞, 0).

In the derivative graph the curve should be above the x-axis in the interval (0, ∞).

So, option C is correct.

Problem 2 :

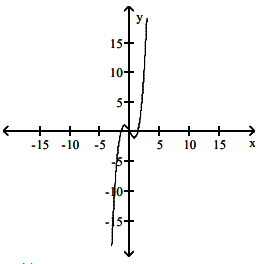
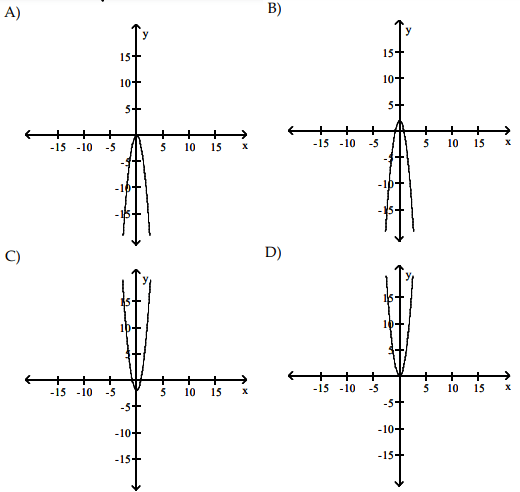
Solution :

Let us assume that the curve is intersecting x-axis on -1 and 1. It is clearly show it intersects the origin also.

So, option C is correct.

Problem 3 :

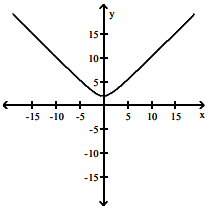
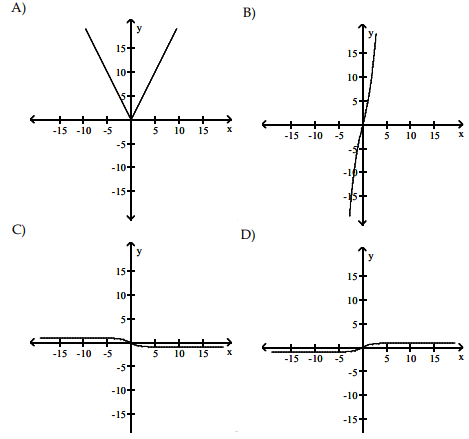
Solution :

Both option B and D satisfies the above conditions, but considering the slope from the given graph it is very closer to 1. So, option D is correct.

Problem 4 :

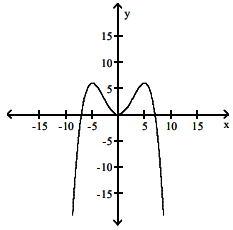
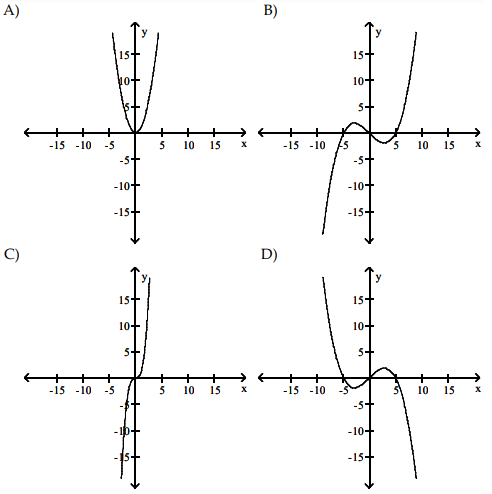
Solution :

So, option D is correct.

Problem 5 :

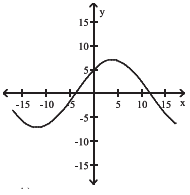
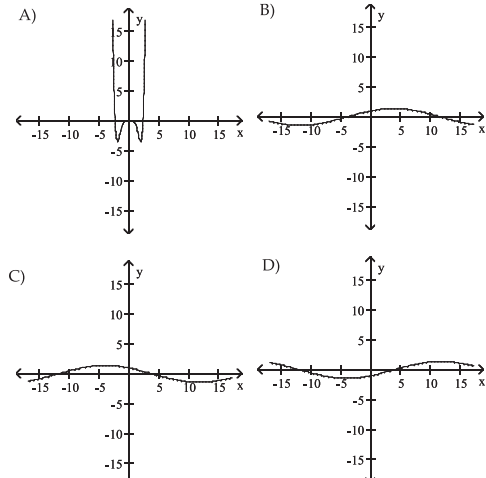
Solution :

So, option C is correct.

Problem 6 :

Given the graph of f, find any values of x which f' is not defined.

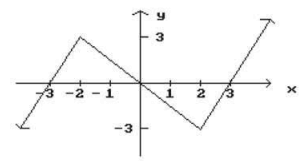
A)  -3, 3    B)  -2, 2      C)  -3, 0, 3    D)  -2, 0, 2

Solution:

At x = -2 and x = 2, we have sharp points. At sharp points its derivative is not defined. So, option B is correct.